AI uses an awful lot of compute.
In the last few years we’ve focused a great deal of our work on making AI use less compute (e.g. Based, Monarch Mixer, H3, Hyena, S4, among others) and run more efficiently on the compute that we have (e.g. FlashAttention, FlashAttention-2, FlashFFTConv). Lately, reflecting on these questions has prompted us to take a step back, and ask two questions:
- What does the hardware actually want?
- And how can we give that to it?
This post is a mixture of practice and philosophy. On the practical side, we’re going to talk about what we’ve learned about making GPUs go brr -- and release an embedded DSL, ThunderKittens, that we’ve built to help us write some particularly speedy kernels (which we are also releasing). On the philosophical side, we’ll briefly talk about how what we’ve learned has changed the way we think about AI compute.
What's in an H100?
For this post, we’re going to focus on the NVIDIA H100 for two reasons. First, it represents an awful lot of new compute going online. Second, we think the trends it implies are going to continue in future generations, and probably from other manufacturers, too. But bear in mind (and we will repeat in case you forget) that most of this post applies in some form to other GPUs, too.

Figure 1: brr
Advance apologies for restating the data sheet, but the details of the hardware are important for the discussion to come. An H100 SXM GPU contains, for our purposes:
- 80 GB of HBM3 with 3 TB/s of bandwidth. (A bit less bandwidth in practice.)
- 50 MB of L2 cache with 12 TB/s of bandwidth, split across the GPU into two 25MB sections connected by a crossbar. (The crossbar sucks.)
- 132 streaming multiprocessors (SM’s), where each has:
- up to 227 KB of shared memory within a 256 KB L1 cache. (Together, these have about 33 TB/s of bandwidth.)
- a tensor memory accelerator (TMA) -- a new chunk of hardware in Hopper that can do asynchronous address generation and fetch memory. It also does other things like facilitate the on-chip memory network (distributed shared memory) but we’re not going to focus on this much, today.
- 4 quadrants, where each quadrant has:
- A warp scheduler
- 512 vector registers (each containing 32 4-byte words)
- A tensor core for matrix multiplies
- A bunch of built-in instructions like sums, multiplies, that operate in parallel on these vector registers.
There’s a lot of other stuff, too (memory controllers, instruction caches, etc) but we don’t care about any of that right now.
All of the compute happens in the SM’s. Most of it happens in the registers.
Great, how do I make it go brr?
Keep the tensor core fed. That’s it.
Wait, really?
Yes. That’s the game.
An H100 GPU has 989 TFLOPs of half-precision matrix multiply compute, and ~60 TFLOPs of “everything else”. So, every cycle the tensor core is in use, you’re getting at least 94% utilization of the hardware. And every cycle the tensor core is not in use, you’re getting no more than 6% utilization of the hardware. Put another way:
Now it turns out that keeping the tensor core fed is easier said than done. We’ve discovered a number of quirks to the hardware that are important to keeping the matrix multiplies rolling. Much of this also applies to non-H100 GPUs, but the H100 is particularly tricky to keep fed so we focus on it here. (The RTX 4090, by comparison, is very easy to work with as illustrated in figure 2.)
- WGMMA instructions are necessary but also really irritating to use.
- Shared memory is not actually that fast and also requires great care.
- Address generation is expensive.
- Occupancy remains helpful, and registers are generally the key resource.

Figure 2: NVIDIA GPUs (H100 and 4090) and their spirit animals (canadian goose and golden retriever puppy).
Let’s go through each of these in order.
WGMMA Instructions
The H100 has a new set of instructions called “warp group matrix multiply accumulate” (wgmma.mma_async in PTX, or HGMMA/IGMMA/QGMMA/BGMMA in SASS). To understand what makes them special, we need to look briefly at how you used to have to use tensor cores. The tensor core instructions available on previous GPUs were wmma.mma.sync and mma.sync instructions. With these instructions a warp of 32 threads on a single quadrant of an SM would synchronously feed their chunk of the data into the tensor core and await the result. Only then could they move on.
Not so with wgmma.mma_async instructions. Here, 128 consecutive threads -- split across all quadrants of the SM -- collaboratively synchronize, and asynchronously launch a matrix multiply directly from shared memory (and optionally also registers.) These warps can then go do other things with their registers while the matrix multiply happens, and await the result whenever they want.
In our microbenchmarks, we found that these instructions are necessary to extract the full compute of the H100. Without them, the GPU seems to top out around 63% of its peak utilization; we suspect this is because the tensor cores want a deep hardware pipeline to keep them fed, even from local resources.
Unfortunately, the memory layouts for these instructions are quite complicated. The unswizzled shared memory layouts suffer from very poor coalescing, and so they require substantial additional bandwidth from L2. The swizzled memory layouts are flat-out incorrectly documented, which took considerable time for us to figure out. They’re also brittle, in that they appear to only work for specific matrix shapes and do not play well with other parts of the wgmma.mma_async instructions. For example, the hardware can transpose sub-matrices on its way to the tensor cores -- but only if the layout is not swizzled.
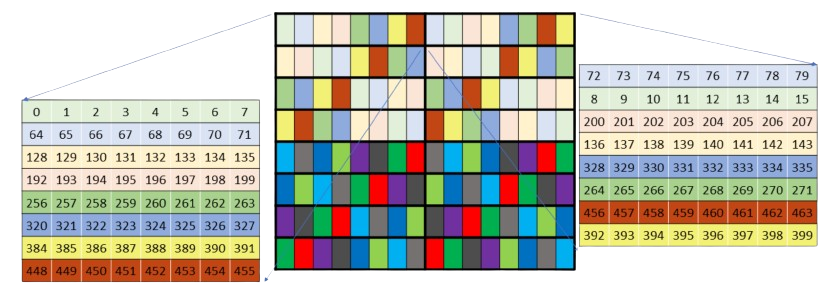
Figure 3: NVIDIA’s lies. This is an extraordinarily misleading representation of the actual 128b swizzled wgmma layout. This diagram cost us three weeks of life that we will not get back, hence the public shaming.
We’ve also found that unswizzled wgmma layouts have both poor memory coalescing as well as bank conflicts. On kernels such as flash attention, TMA and the L2 cache are both fast enough so as to hide these problems reasonably well. But to make the full use of the hardware, memory request must be coalesced and bank conflicts avoided, and then controlling layouts very carefully becomes critical.
Despite these pains, these instructions really are necessary to make full use of the H100. Without them, you’ve already lost 37% of the potential performance of the GPU!
Shared memory
Shared memory appears to have a single-access latency of around 30 cycles (this matches our observations, too). That doesn’t sound like much, but in that time the SM’s tensor cores could have done almost two full 32x32 square matrix multiplies.
In previous work (like Flash Attention), we’ve focused more on the HBM-SRAM bottleneck. And indeed: this really used to be the bottleneck! But as HBM has gotten faster and the tensor cores continue to grow out of proportion with the rest of the chip, even relatively small latencies like those from shared memory have also become important to either remove or hide.
Shared memory can be tricky to work with because it is “banked” into 32 separate stores of memory. If one is not careful, this can lead to something called “bank conflicts”, where the same memory bank is being asked to simultaneously provide multiple different pieces of memory. This leads to requests being serialized, and in our experience this can disproportionately slow down a kernel -- and the register layouts required by wgmma and mma instructions would naively suffer from these bank conflicts. The solution is to rearrange shared memory with various “swizzling” patterns so as to avoid these conflicts, but it is an important detail to get right.
More generally, we have found it very valuable to avoid movement between registers and shared memory when possible, and otherwise to use the built-in hardware (wgmma and TMA instructions) to do data movement asynchronously when possible. Synchronous movement using the actual warps is a worst-case fallback with the greatest generality.
Address Generation
One interesting quirk of the H100 is that the tensor cores and memory are both fast enough that merely producing the memory addresses to fetch takes a substantial fraction of the resources of the chip. (This is even more the case when complicated interleaved or swizzling patterns are added in.)
NVIDIA appears to understand this, as they have bestowed on us the Tensor Memory Accelerator (or TMA, as it likes to be called). TMA allows you to specify a multi-dimensional tensor layout in global and shared memory, tell it to asynchronously fetch a subtile of that tensor, and trip a barrier when it’s done. This saves all of the address generation costs, and additionally makes it much easier to construct pipelines.
We have found TMA to be, like wgmma.mma_async, completely indispensable in achieving the full potential of the H100. (Probably moreso than wgmma, in our experience.) It saves register resources and instruction dispatches, and also has useful features such as the ability to perform reductions onto global memory asynchronously, too -- this is particularly useful in complex backwards kernels. As with wgmma, the main quirk of it is that its swizzling modes are a bit difficult to decipher without some reverse engineering, but we had substantially less pain on this point.
Occupancy
For those newer to CUDA, occupancy refers to the number of co-scheduled threads on the exact same execution hardware. Each cycle, the warp scheduler on that quadrant of the SM will try to issue an instruction to a warp of threads that are ready for an instruction. NVIDIA uses this model because it can enable the hardware to be more easily kept full. For example, while one warp of threads is waiting for a matrix multiply, another can receive an instruction to use the fast exponential hardware.
In some ways, the H100 is less reliant on occupancy than previous generations of the hardware. The asynchronous features of the chip mean that even a single instruction stream can keep many parts of the hardware busy -- fetching memory, running matrix multiplies, doing shared memory reductions, and still simultaneously running math on the registers.
But occupancy is very good at hiding both sins and sync’s. A perfectly designed pipeline might run reasonably fast even without any additional occupancy, but our observations suggest that NVIDIA really has designed their GPUs with occupancy in mind. And there are enough synchronizations -- and enough ways to make mistakes -- that finding ways to increase occupancy has, in our experience, usually yielded good returns at increasing the realized utilization of the hardware.
Finally, while occupancy is merely useful on the H100, we have found it to be increasingly important on the A100 and RTX 4090, respectively, likely because they rely increasingly on synchronous instruction dispatches, relative to the H100.
ThunderKittens
Based on the above, we asked ourselves how we might make it easier to write the kinds of kernels we care about while still extracting the full capabilities of the hardware. Motivated by a continuing proliferation of new architectures within the lab (and the fact that Flash Attention is like 1200 lines of code), we ended up designing a DSL embedded within CUDA -- at first for our own internal use.
But then we decided it was useful enough that, with love in our hearts, we cleaned it up and have released it for you. ThunderKittens is that embedded DSL. It is named ThunderKittens because we think kittens are cute, and also we think it is funny to make you type kittens:: in your code.

Figure 4: A ThunderKitten. Look at her big eyes! Are you not be entranced!?!?
It is meant to be as simple as possible, and contains four templated types:
- Register tiles -- 2D tensors on the register file.
- Register vectors -- 1D tensors on the register file.
- Shared tiles -- 2D tensors in shared memory.
- Shared vectors -- 1D tensors in shared memory.
Tiles are parameterized by a height, width, and layout. Register vectors are parameterized by a length and a layout, and shared vectors just by a length. (They don’t generally suffer from bank conflicts.)
We also give operations to manipulate them, either at the warp level or at the level of a collaborative group of warps. Examples include:
- Initializers -- zero out a shared vector, for example.
- Unary ops, like exp
- Binary ops, like mul
- Row / column ops, like a row_sum
Since ThunderKittens is embedded within CUDA (contrasting libraries like Triton which we also love very much and rely on heavily), the abstractions fail gracefully. If it’s missing something, just extend it to do what you want!
To show an example of these primitives in action, consider Tri’s lovely flash attention -- a beautiful algorithm, but complicated to implement in practice, even on top of NVIDIA’s wonderful Cutlass library.
Here's a simple forward flash attention kernel for an RTX 4090, written in ThunderKittens.
#define NUM_WORKERS 16 // This kernel uses 16 workers in parallel per block, to help issue instructions more quickly.
using namespace kittens; // this kernel only handles headdim=64 for simplicity. Also n should be a multiple of 256 here.
__global__ void attend_ker64(int n, const bf16* __restrict__ __q__, const bf16* __restrict__ __k__, const bf16* __restrict__ __v__, bf16* __o__) {
auto warpid = kittens::warpid();
auto block_start = blockIdx.x*(n*64);
const bf16 *_q = __q__ + block_start, *_k = __k__ + block_start, *_v = __v__ + block_start;
bf16 *_o = __o__ + block_start;
extern __shared__ alignment_dummy __shm[]; // this is the CUDA shared memory
shared_allocator al((int*)&__shm[0]);
// K and V live in shared memory -- this is about all that will fit.
st_bf_1x4<ducks::st_layout::swizzle> (&k_smem)[NUM_WORKERS] = al.allocate<st_bf_1x4<ducks::st_layout::swizzle>, NUM_WORKERS>();
st_bf_1x4<ducks::st_layout::swizzle> (&v_smem)[NUM_WORKERS] = al.allocate<st_bf_1x4<ducks::st_layout::swizzle>, NUM_WORKERS>();
// Initialize all of the register tiles.
rt_bf_1x4<> q_reg, k_reg, v_reg; // v_reg need to be swapped into col_l
rt_fl_1x1<> att_block;
rt_bf_1x1<> att_block_mma;
rt_fl_1x4<> o_reg;
rt_fl_1x1<>::col_vec max_vec_last, max_vec; // these are column vectors for the attention block
rt_fl_1x1<>::col_vec norm_vec_last, norm_vec; // these are column vectors for the attention block
int qo_blocks = n / (q_reg.rows*NUM_WORKERS), kv_blocks = n / (q_reg.rows*NUM_WORKERS);
for(auto q_blk = 0; q_blk < qo_blocks; q_blk++) {
// each warp loads its own Q tile of 16x64, and then multiplies by 1/sqrt(d)
load(q_reg, _q + (q_blk*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
mul(q_reg, q_reg, __float2bfloat16(0.125f)); // temperature adjustment
// zero flash attention L, M, and O registers.
neg_infty(max_vec); // zero registers for the Q chunk
zero(norm_vec);
zero(o_reg);
// iterate over k, v for these q's that have been loaded
for(auto kv_idx = 0; kv_idx < kv_blocks; kv_idx++) {
// each warp loads its own chunk of k, v into shared memory
load(v_smem[warpid], _v + (kv_idx*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
load(k_smem[warpid], _k + (kv_idx*NUM_WORKERS + warpid)*q_reg.num_elements, q_reg.cols);
__syncthreads(); // we need to make sure all memory is loaded before we can begin the compute phase
// now each warp goes through all of the subtiles, loads them, and then does the flash attention internal alg.
for(int subtile = 0; subtile < NUM_WORKERS; subtile++) {
load(k_reg, k_smem[subtile]); // load k from shared into registers
zero(att_block); // zero 16x16 attention tile
mma_ABt(att_block, q_reg, k_reg, att_block); // Q@K.T
copy(norm_vec_last, norm_vec);
copy(max_vec_last, max_vec);
row_max(max_vec, att_block, max_vec); // accumulate onto the max_vec
sub_row(att_block, att_block, max_vec); // subtract max from attention -- now all <=0
exp(att_block, att_block); // exponentiate the block in-place.
sub(max_vec_last, max_vec_last, max_vec); // subtract new max from old max to find the new normalization.
exp(max_vec_last, max_vec_last); // exponentiate this vector -- this is what we need to normalize by.
mul(norm_vec, norm_vec, max_vec_last); // and the norm vec is now normalized.
row_sum(norm_vec, att_block, norm_vec); // accumulate the new attention block onto the now-rescaled norm_vec
div_row(att_block, att_block, norm_vec); // now the attention block is correctly normalized
mul(norm_vec_last, norm_vec_last, max_vec_last); // normalize the previous norm vec according to the new max
div(norm_vec_last, norm_vec_last, norm_vec); // normalize the previous norm vec according to the new norm
copy(att_block_mma, att_block); // convert to bf16 for mma_AB
load(v_reg, v_smem[subtile]); // load v from shared into registers.
rt_bf_1x4<ducks::rt_layout::col> &v_reg_col = swap_layout_inplace(v_reg); // this is a reference and the call has invalidated v_reg
mul_row(o_reg, o_reg, norm_vec_last); // normalize o_reg in advance of mma_AB'ing onto it
mma_AB(o_reg, att_block_mma, v_reg_col, o_reg); // mfma onto o_reg with the local attention@V matmul.
}
__syncthreads(); // we need to make sure all warps are done before we can start loading the next kv chunk
}
store(_o + (q_blk*NUM_WORKERS + warpid)*q_reg.num_elements, o_reg, q_reg.cols); // write out o. compiler has an issue with register usage if d is made constexpr q_reg.rows :/
}
}
Altogether, this is about 60 lines of CUDA sitting at 75% hardware utilization -- and while it is fairly dense, most of the complexity is in the algorithm, rather than in swizzling patterns or register layouts. And what of all of the complexity of TMA, WGMMA, swizzling modes, and descriptors? Here’s a FlashAttention-2 forward pass for the H100, written with ThunderKittens.
template<int D>
__global__ __launch_bounds__((NUM_WORKERS)*kittens::WARP_THREADS, 2)
void fwd_attend_ker_dim(int N, const CUtensorMap* tma_q, const CUtensorMap* tma_k, const CUtensorMap* tma_v, CUtensorMap* tma_o) {
extern __shared__ int __shm[]; // this is the CUDA shared memory
tma_swizzle_allocator al((int*)&__shm[0]);
constexpr int tile_width = fwd_attend_ker_tile_dims<D>::tile_width; // constants
constexpr int qo_height = fwd_attend_ker_tile_dims<D>::qo_height;
constexpr int kv_height = fwd_attend_ker_tile_dims<D>::kv_height;
st_bf<qo_height, tile_width, layout_q> (&q_smem) [NUM_WARPGROUPS] = al.allocate<st_bf<qo_height, tile_width, layout_q>, NUM_WARPGROUPS>();
st_bf<kv_height, tile_width, layout_k> (&k_smem)[2][NUM_WORKERS_KV] = al.allocate<st_bf<kv_height, tile_width, layout_k>, 2, NUM_WORKERS_KV>();
st_bf<kv_height, tile_width, layout_v> (&v_smem)[2][NUM_WORKERS_KV] = al.allocate<st_bf<kv_height, tile_width, layout_v>, 2, NUM_WORKERS_KV>();
int tic = 0, toc = 1;
rt_fl<1, kv_height> att_block;
rt_bf<1, kv_height> att_block_mma;
rt_fl<1, qo_height> o_prev;
col_vec<rt_fl<1, kv_height>> max_vec_last, max_vec;
col_vec<rt_fl<1, kv_height>> norm_vec_last, norm_vec;
int warpid = kittens::warpid();
int warpgroupid = warpid/kittens::WARPGROUP_WARPS;
int kv_blocks = N / (NUM_WORKERS_KV*k_smem[0][0].rows);
__shared__ uint64_t qsmem_barrier, kvsmem_barrier;//, vsmem_barrier;
int q_phasebit = 0;
int kv_phasebit = 0;
if (threadIdx.x == 0) {
tma::init_barrier<st_bf<qo_height, tile_width, layout_q>, NUM_WARPGROUPS>(qsmem_barrier, 1);
tma::init_barrier<st_bf<kv_height, tile_width, layout_k>, NUM_WORKERS_KV*2>(kvsmem_barrier, 1);
}
if (warpid == 0) {
for (int wg = 0; wg < NUM_WORKERS/kittens::WARPGROUP_WARPS; wg++) { // load q
int tile_idx = (blockIdx.y * NUM_WARPGROUPS * gridDim.x) + (blockIdx.x * NUM_WARPGROUPS) + wg;
tma::load_async((q_smem[wg]), tma_q, qsmem_barrier, tile_idx);
}
for (int w = 0; w < NUM_WORKERS_KV; w++) { // load k, v
int tile_idx = (blockIdx.y * NUM_WORKERS_KV * kv_blocks) + (0 * NUM_WORKERS_KV) + w;
tma::load_async((k_smem[tic][w]), tma_k, kvsmem_barrier, tile_idx);
tma::load_async((v_smem[tic][w]), tma_v, kvsmem_barrier, tile_idx);
}
}
neg_infty(max_vec); // zero registers for the Q chunk
zero(norm_vec);
zero(o_prev);
__syncthreads();
tma::arrive_and_wait(qsmem_barrier, q_phasebit);
q_phasebit ^= 1;
if constexpr (D == 64) { warpgroup::mul(q_smem[warpgroupid], q_smem[warpgroupid], __float2bfloat16(0.125f)); }
else { warpgroup::mul(q_smem[warpgroupid], q_smem[warpgroupid], __float2bfloat16(0.08838834764f)); }
for (auto kv_idx = 0; kv_idx < kv_blocks; kv_idx++, tic ^= 1, toc ^= 1) {
tma::arrive_and_wait(kvsmem_barrier, kv_phasebit);
kv_phasebit ^= 1;
__syncthreads();
if (warpid == 0) {
tma::set_bytes(kvsmem_barrier, 2 * NUM_WORKERS_KV * k_smem[0][0].num_elements * sizeof(bf16));
if (kv_idx + 1 < kv_blocks) {
for (int w = 0; w < NUM_WORKERS_KV; w++) {
int tile_idx = (blockIdx.y * NUM_WORKERS_KV * kv_blocks) + ((kv_idx + 1) * NUM_WORKERS_KV) + w;
tma::load_async((k_smem[toc][w]), tma_k, kvsmem_barrier, tile_idx);
tma::load_async((v_smem[toc][w]), tma_v, kvsmem_barrier, tile_idx);
}
}
}
warpgroup::mma_fence(att_block);
warpgroup::mm_ABt(att_block, q_smem[warpgroupid], k_smem[tic][0]);
warpgroup::mma_commit_group();
copy(norm_vec_last, norm_vec);
copy(max_vec_last, max_vec);
warpgroup::mma_async_wait();
row_max(max_vec, att_block, max_vec); // accumulate onto the max_vec
sub_row(att_block, att_block, max_vec);
exp(att_block, att_block);
sub(max_vec_last, max_vec_last, max_vec);
exp(max_vec_last, max_vec_last);
mul(norm_vec, norm_vec, max_vec_last);
row_sum(norm_vec, att_block, norm_vec); // accumulate onto the norm_vec
div_row(att_block, att_block, norm_vec);
mul(norm_vec_last, norm_vec_last, max_vec_last);
div(norm_vec_last, norm_vec_last, norm_vec);
copy(att_block_mma, att_block); // convert to bf16 for mma
mul_row(o_prev, o_prev, norm_vec_last); // normalize o_prev in advance of mma'ing onto it
warpgroup::mma_fence(o_prev);
warpgroup::mma_AB(o_prev, att_block_mma, v_smem[tic][0]);
warpgroup::mma_commit_group();
}
auto (*o_smem) = reinterpret_cast<st_bf<qo_height, tile_width, layout_o>(*)>(q_smem); // reuse q memory
warpgroup::store(o_smem[warpgroupid], o_prev);
__syncthreads();
if (warpid % 4 == 0) { // store o
int tile_idx = (blockIdx.y * NUM_WARPGROUPS * gridDim.x) + (blockIdx.x * NUM_WARPGROUPS) + warpgroupid;
tma::store_async(tma_o, (o_smem[warpgroupid]), tile_idx);
tma::store_commit_group();
}
tma::store_async_wait();
}
So how does it do?
This kernel is just 100 lines, and it actually outperforms FlashAttention-2 on the H100 by about 30%. ThunderKittens takes care of wrapping up the layouts and instructions, and gives you a mini-pytorch to play with on the GPU.

Figure 5: FA2 (via Pytorch) versus TK for a wide range of configs on the H100 SXM.
We also release kernels for Based linear attention and other forthcoming architectures, too. Our Based linear attention kernel runs at 215 TFLOPs (or more than 300 TFLOPs when the recompute inherent in the algorithm is considered). And while linear attention is of course theoretically more efficient, historically, they have been dramatically less efficient on real hardware. So we feel this could open up a broad range of high-throughput applications -- more to come on this point later.
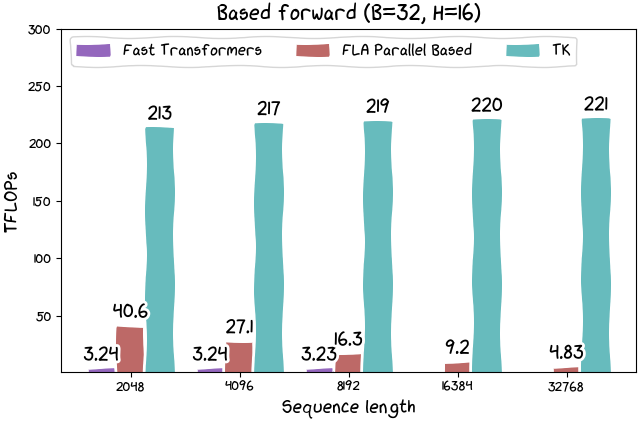
Figure 6: Linear attention can be quite quick with TK!
If this seems up your alley, feel free to play with it!
Tiles Seem Like a Good Idea
In our view, what has made ThunderKittens work well for us is that it does not try to do everything. CUDA is indeed far more expressive than ThunderKittens. ThunderKittens is small and dumb and simple.

Figure 7: the main message of this blog post.
But ThunderKittens has good abstractions -- small tiles -- that match where both AI and hardware are going. ThunderKittens doesn’t support any dimension less than 16. But in our view, this doesn’t really matter, since the hardware doesn’t particularly want to, either. And we ask: if your matrix multiply is smaller than 16x16, are you sure what you’re doing is AI?
From a philosophical point of view, we think a frame shift is in order. A “register” certainly shouldn’t be a 32-bit word like on the CPUs of old. And a 1024-bit wide vector register, as CUDA uses, is certainly a step in the right direction. But to us a “register” is a 16x16 tile of data. We think AI wants this -- after all this time, it’s still just matrix multiplies, reductions, and reshapes. And we think the hardware wants this, too -- small matrix multiplies are just begging for hardware support beyond just the systolic mma.
In fact, more broadly we believe we should really reorient our ideas of AI around what maps well onto the hardware. How big should a recurrent state be? As big can fit onto an SM. How dense should the compute be? No less so than what the hardware demands. An important future direction of this work for us is to use our learnings about the hardware to help us design the AI to match.
Tiles Seem Pretty General
Coming soon -- ThunderKittens on AMD hardware!