Dec 11, 2023 · 8 min read
Monarchs and Butterflies: Towards Sub-Quadratic Scaling in Model Dimension
Dan Fu, with work from past & present students of Hazy Research.

Over the past few years, a line of work in our lab has been to look at how we can make a core operation in ML models more efficient: matrix multiplication. Matrix multiply operations take up a majority of FLOPs and runtime in a model (up to 99% of the FLOPs, in one analysis). A major portion of this matrix multiply cost, especially for large models, is in the MLP layers and projection layers—which have cost that grows quadratically in the model dimension.
This blog post will give a brief survey of a line of work from our lab that has started to chip away at this quadratic cost—and has started to go towards models that are sub-quadratic in model dimension. If we can develop models that have similar quality but that scale sub-quadratically, we could start seeing some radically more efficient models.
This work has deep connections to theory, hardware, and the computational primitives behind the Fast Fourier Transform. As an aside, it also has close connections to our work on models that are sub-quadratic in sequence length, but that’s a blog post for another day. As always, we build on the shoulders of giants who have been looking into deep connections between Butterflies and ML for years (check out Mark Tygert’s work and work out of Lexing Ying’s group).
This blog post is part of a series of surveys on building blocks in foundation models and AI systems (associated with an upcoming NeurIPS keynote). If you’re interested in things like this, come join our community on GitHub!
Sparsity: One Attack for Efficiency
Matrix multiply is one of the core operations of modern ML models. From the ConvNets of the 2010’s to today’s Transformers, matrix multiply operations take up most of the compute and wall-clock runtime of ML models.
Naturally, reducing the cost of matrix multiply operations has been of major interest in machine learning. A natural vector of attack is sparsity – the idea that instead of having full matrices, you can zero out major portions and skip them during computation. It’s been explored to great effect in the community – check out Du et al, Beltagy et al, Frankle & Carbin, Han et al, Dong et al, among others. Visually, we let the blue squares be learnable parameters, and the white squares be zeros:

A sparse matrix. White squares are zeros, dark blue are learnable parameters.
There’s good evidence that some approach like this should work. Post-hoc analyses of trained LLMs have found that many of the activations are sparse after training, so why not just build this in from the get-go?
Arbitrary sparsity has two challenges: the quality-compute tradeoff, and poor hardware support.
Quality-Compute Tradeoff
The natural first question about sparsity is – what do we lose from using sparse approaches? Can we still match in quality? Put another way – are our sparse matrices capable of capturing the transforms that we want?
In our lab, we look at this from a theoretically-driven perspective. Can sparse matrices capture well-known structured linear transforms, going back to a paper from Albert Gu and Chris De Sa, and building on canonical work in structured matrices. Here, we’ve displayed convolutions and Fourier/cosine transforms as one family of transforms you might want to represent:

Structured linear maps.
It's not clear that arbitrary sparse matrices can capture these. There's a lot of structure, but no regions of zeros!
Hardware Support
The second challenge with sparsity is hardware support. Modern GPUs (and other ML accelerators like TPUs) have specialized hardware units for dense matrix-matrix multiply called tensor cores. Tensor cores can compute matrix-matrix multiply at 16x the FLOP rate of general arithmetic operations:
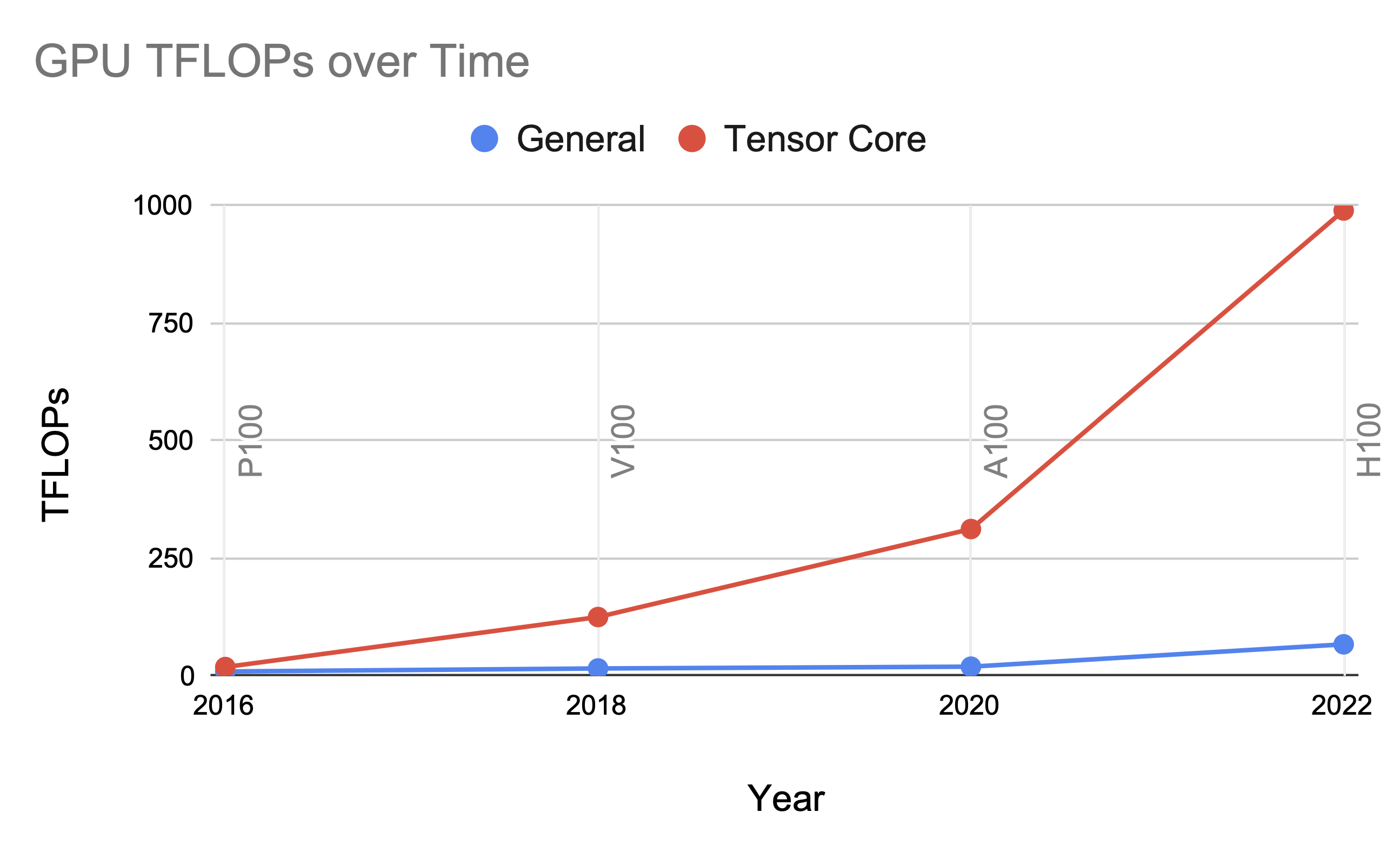
FLOPs of general arithmetic vs. tensor cores (matrix-matrix multiply) over time.
This trend is pretty fundamental to how we know how to build hardware – systolic arrays are a reliable way to get a lot of compute on chip. And the trend is accelerating: from 8x speedup on V100 to 16x on A100/H100 (and possibly more in future hardware generations).
Arbitrary sparsity patterns can’t use these dense matrix multiply units, so they’re at a major disadvantage from wall-clock time and hardware utilization.1
Butterflies and Kaleidoscopes
In our lab, we have had a line of work over the past few years studying structured sparsity. The basic idea is this: what if we use sparsity patterns inspired by specific linear transforms that can be computed efficiently, such as the Fast Fourier Transform (FFT)? Does this offer an expressive class of sparse matrices, and can we make them efficient on hardware?
Our early explorations into this took inspiration from the FFT. For the uninitiated, the FFT is a powerful linear transform with many applications in signal processing, controls, and engineering. Linear transforms naively require quadratic compute, but the FFT admits a divide-and-conquer algorithm (going back to the 60’s), which allows us to compute it efficiently in time:
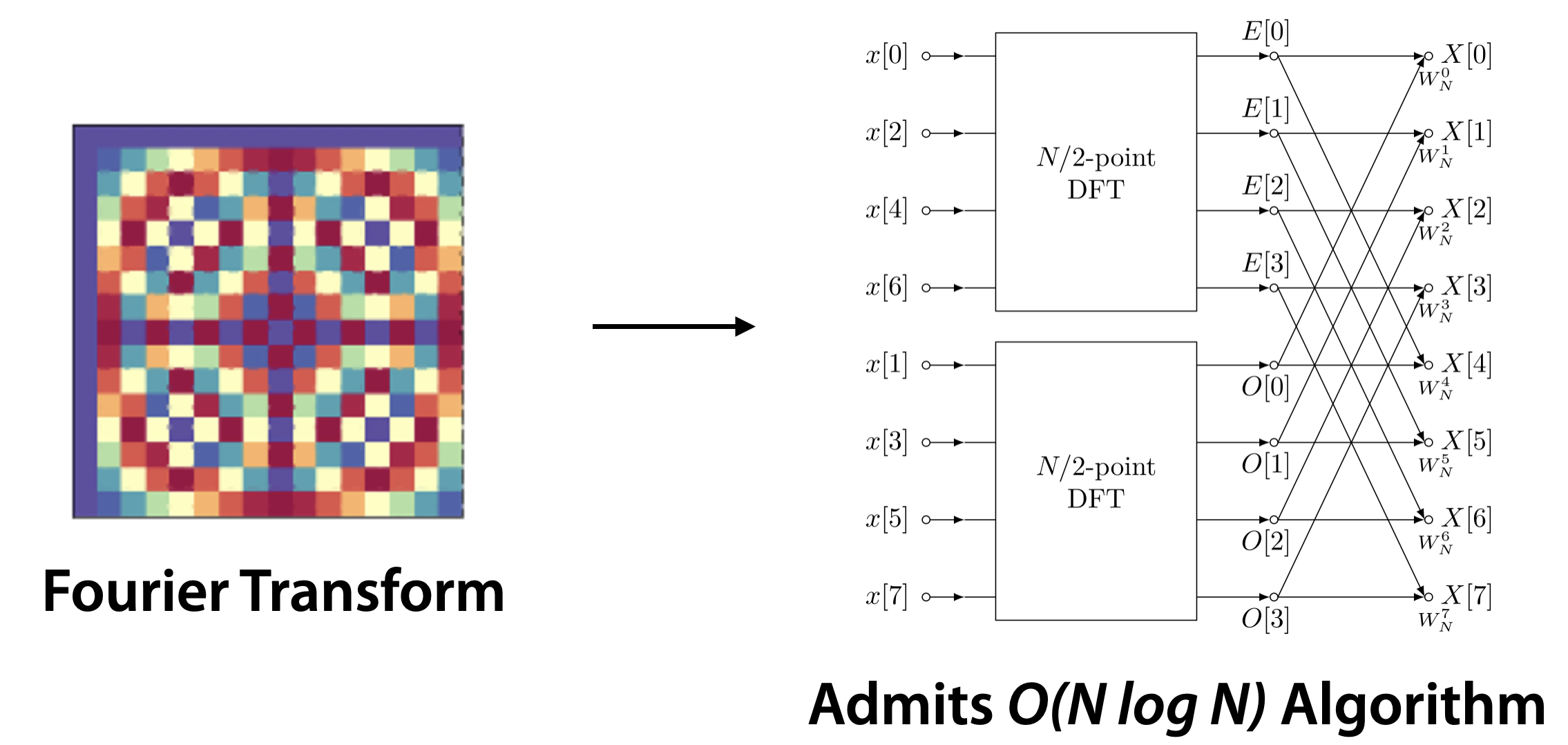
The Fourier transforms admits an divide and conquer algorithm.
Our early explorations into this took the Butterfly compute pattern of the FFT (that divide-and-conquer algorithm on the right) and tried to generalize it. The Butterfly transform is the compute pattern shown on the right there – a set of permutations and adjustment factors.
In a series of papers [1, 2, 3] from our lab spanning two PhDs and a postdoc (Albert, Tri, Beidi), we took a look at what happens if you take this basic compute pattern, but learn the adjustment factors instead of using the fixed values from the FFT. A learnable Butterfly pattern, if you will:
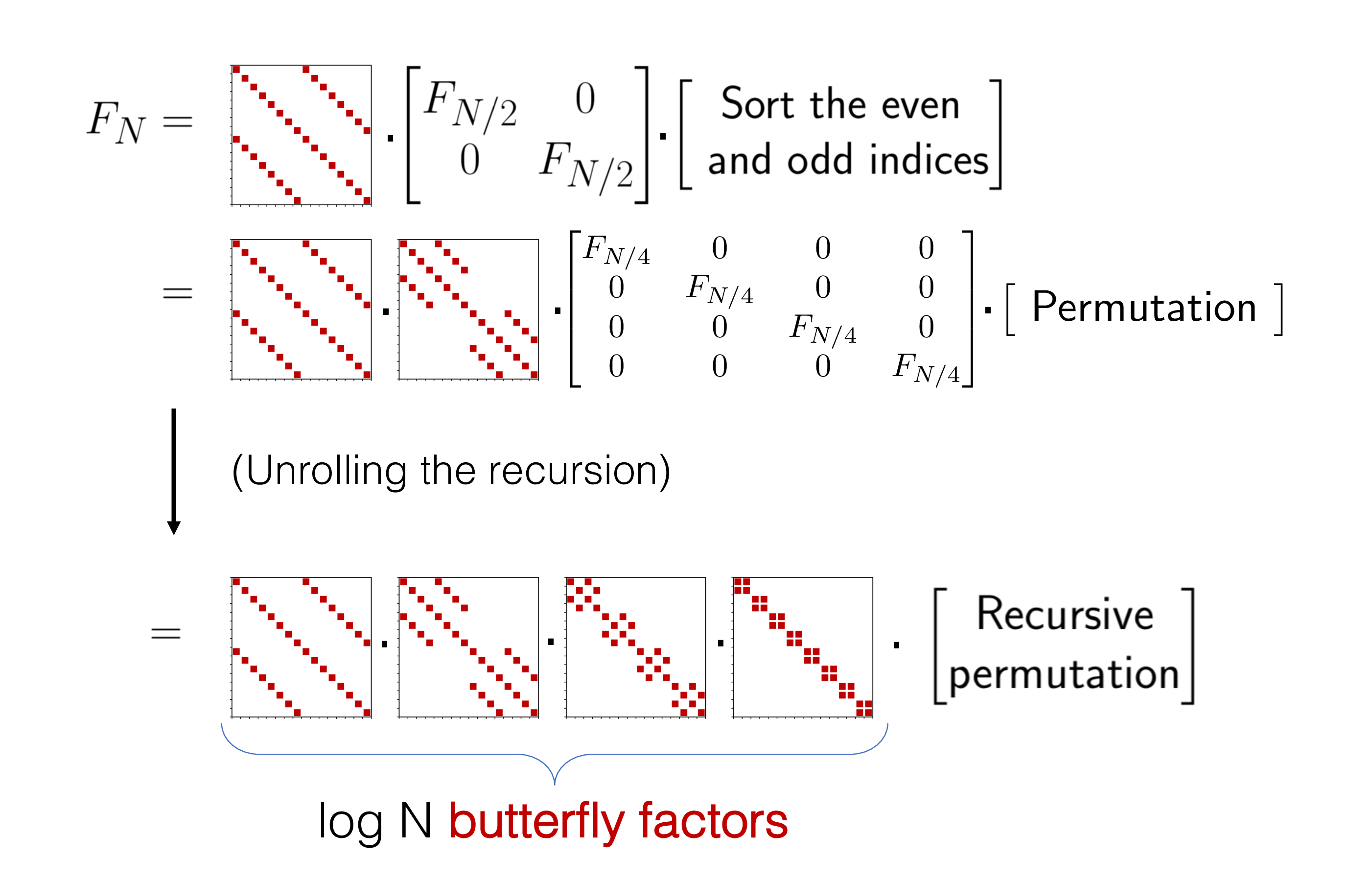
Learnable Butterfly patterns, generalizing the FFT.
These learnable structured sparse matrices could go a long way to matching dense matrices in quality. For example, GPT-2 medium on WikiText (Pixelfly uses learnable Butterfly transforms):
| Model | WikiText-103 (ppl ↓) | Params | FLOPs |
|---|---|---|---|
| GPT-2-medium | 20.9 | 345M | 168G |
| Pixelfly-GPT-2-medium | 21.0 | 203M | 27G |
And some recent work from the community has built on these ideas to do LORA-style fine-tuning after the fact!
But there was still a problem: although we were starting to get a handle on quality, many of these methods still had low hardware efficiency (e.g., less than 2% FLOP utilization).
From Butterflies to Monarchs
Enter Monarch matrices (see Monarch, and Monarch Mixer oral at NeurIPS this week!). Monarch matrices rewrite the Butterfly compute pattern above by refactoring into permutations and block-diagonal matrices (P stands for permutation here):
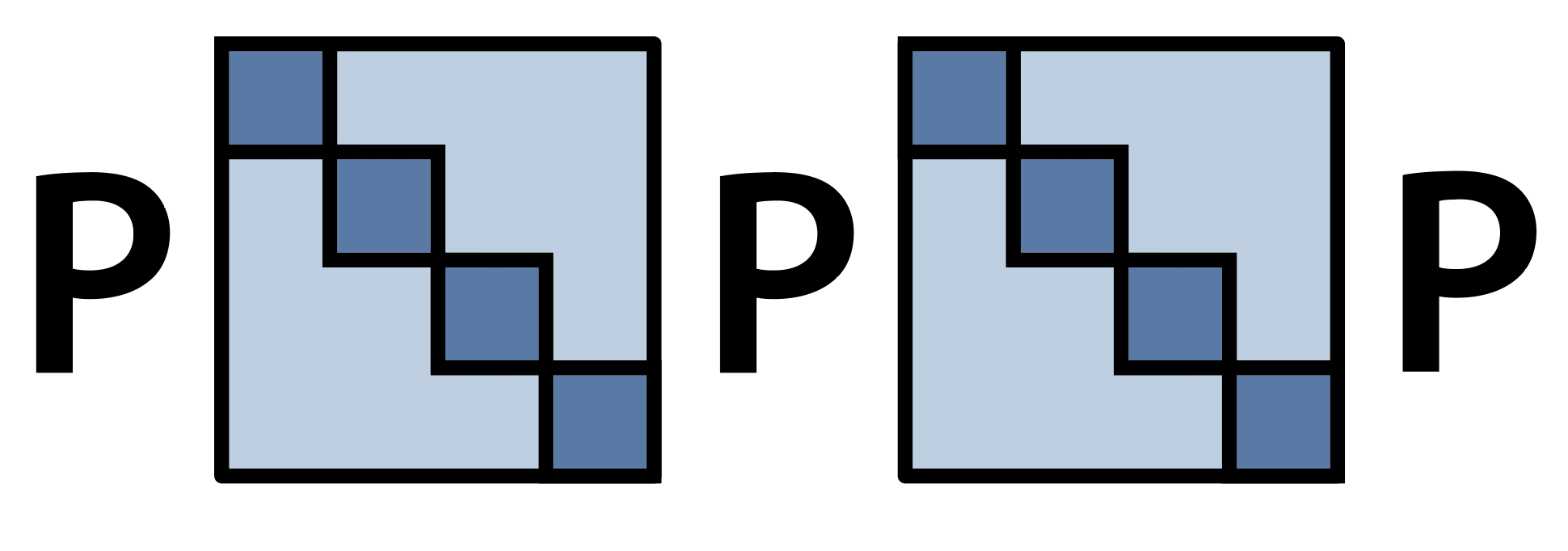
Monarch matrices are block-diagonal matrices interleaved with permutations.
This compute pattern takes the Butterfly factors from before, and rewrites it into a series of permutations and block-diagonal matrices. It’s the same Butterfly factors as before, with the permutations rolled out.
Critically: the block-diagonal matrices map efficiently onto tensor cores, which means that we can use dense matrix multiply units!
With Monarch matrices, Tri and Beidi were able to show strong performance and wall-clock speedup in sparse-to-dense training. The first 90% of the training replaces linear layers with sparse Monarch matrices, and the last 10% goes up to full dense matrices.
On OpenWebText, this results in end-to-end speedup:
| Model | OpenWebText (ppl ↓) | Speedup |
|---|---|---|
| GPT-2-medium | 18.0 | 1.0x |
| Monarch-GPT-2-medium | 18.0 | 2.0x |
And in our latest work, Monarch Mixer, we took this idea one step further. We were able to achieve full end-to-end sparse training. We also used Monarch matrices to replace attention as well, building on our work in efficient long sequence models (but that’s another blog post).
We focused on BERT training in Monarch Mixer – matching BERT quality with up to 27% fewer parameters:
| Model | Average GLUE Score |
|---|---|
| BERT-base (110M) | 79.6 |
| M2-BERT-base (80M) | 79.9 |
| BERT-large (340M) | 82.1 |
| M2-BERT-large (260M) | 82.2 |
And because we replaced attention with Monarch matrices as well, we were able to achieve up to 9.1x wall-clocks speedup on long sequences:
| Model | Seq Len 512 | Seq Len 4096 |
|---|---|---|
| BERT-base (110M) | 1.0x | 1.0x |
| M2-BERT-base (80M) | 1.9x | 9.1x |
Check out the paper for more results – matching ViT-b with half the parameters, and matching GPT performance without any MLPs at all (we replaced them with the identity function).
Monarch matrices are also the same basic idea behind FlashFFTConv. Since Monarch matrices generalize the FFT and are hardware-efficient, they form a natural opportunity to speed up the FFT! In FlashFFTConv, we use this to improve the FLOP utilization of convolution-based language models. Check out our blog post on FlashFFTConv to read more!
What's Next
This has just been a short survey of approaches to improve the efficiency of matrix multiply in ML models, and move us a few steps closer towards a world where model cost scales sub-quadratically in dimension.
There’s many more interesting questions to answer here. Can we understand more deeply what happens in the MLP layers in large language models? How far can we push these ideas of sparsity?
If you’re interested in these ideas, please reach out – we would love to hear from you and discuss research!
This is part of a series of blog posts tied to an upcoming NeurIPS keynote on Building Blocks for Foundation Models – check out our GitHub for more resources and to get involved!
Dan Fu: danfu@cs.stanford.edu
- There has been some support for sparsity in recent hardware iterations, but they require very specific sparsity patterns (which encounter the problems with quality-compute tradeoff mentioned earlier).↩