LoLCATs Blog Part 2: How to Linearize LLMs for Me and You

Full team: Michael, Simran, Rahul, Alan, Ben, Aaryan, Krithik, and Chris Ré.

Paper | Code | Models | Part 1

---

In Part 1, we shared LoLCATs, a new way to linearize high-quality LLMs on much more accessible compute. We’ll now share more about the method and our results.

What’s linearizing? And is linearizing all we need?

When we started working on LoLCATs, we really just wanted 7B+ LLMs with three things: competitive quality, subquadratic efficiency, and the ability for us to actually create them.

There's been a ton of exciting recent work on high quality and highly-efficient architectures, but we still don't have ways to easily scale these up, especially to modern LLM regimes. Doing things the typical way---i.e., training new architectures from scratch---would mean training 7B+ parameters on trillions of tokens (so far, 1 - 15 trillion!). We didn't have this compute budget lying around (remember, we're fighting for one of 64 A100s).

Alternatively, we could "linearize" (also known before as "linear conversion" or "continued pretraining"). We'd start with existing pretrained Transformers, replace their self-attentions with efficient analogs (such as linear attentions), and continue training to adjust to the transplanted layers. In our own work, we started exploring linearizing LLMs in Hedgehog, linearizing Llama 2 7B for a summarization task. Excitingly, folks at TRI showed how to linearize Llama 2 7B and Mistral 7B to recover general zero-shot LM capabilities! And our lab alums more recently shared similar work distilling 1.3B and 8B Transformer LLMs into their favorite Mamba architectures.

Unfortunately, linearizing was not all we needed just yet. The proposed ways to linearize LLMs were still too expensive and left quality on the table. All prior methods involved fully training 7B parameter LLMs on billions of tokens after swapping attentions. Their linearized models also underperformed the original Transformers by 1.7 to 8.0 points on popular LM Eval tasks (up to 28.2 points on MMLU!). Could we close this gap?

---

LoLCATs: adding more L's to get more W's

In short, we could. Our main idea was to add three simple concepts to linearizing Transformers:

1. Learnable (Linear) Attentions
2. Low-rank Adaptation
3. Layer-wise Optimization

1. Learning (Linear) Attentions

We first had to pick what to swap out softmax attentions for. To make linearizing easier, we wondered if we could simply use linear attentions, which would give us subquadratic efficiency while also being architecturally similar.

If you know... you know.

While simple, prior works have suggested this might not be enough, where linear attentions often struggle to match softmax attention in expressivity ¹²

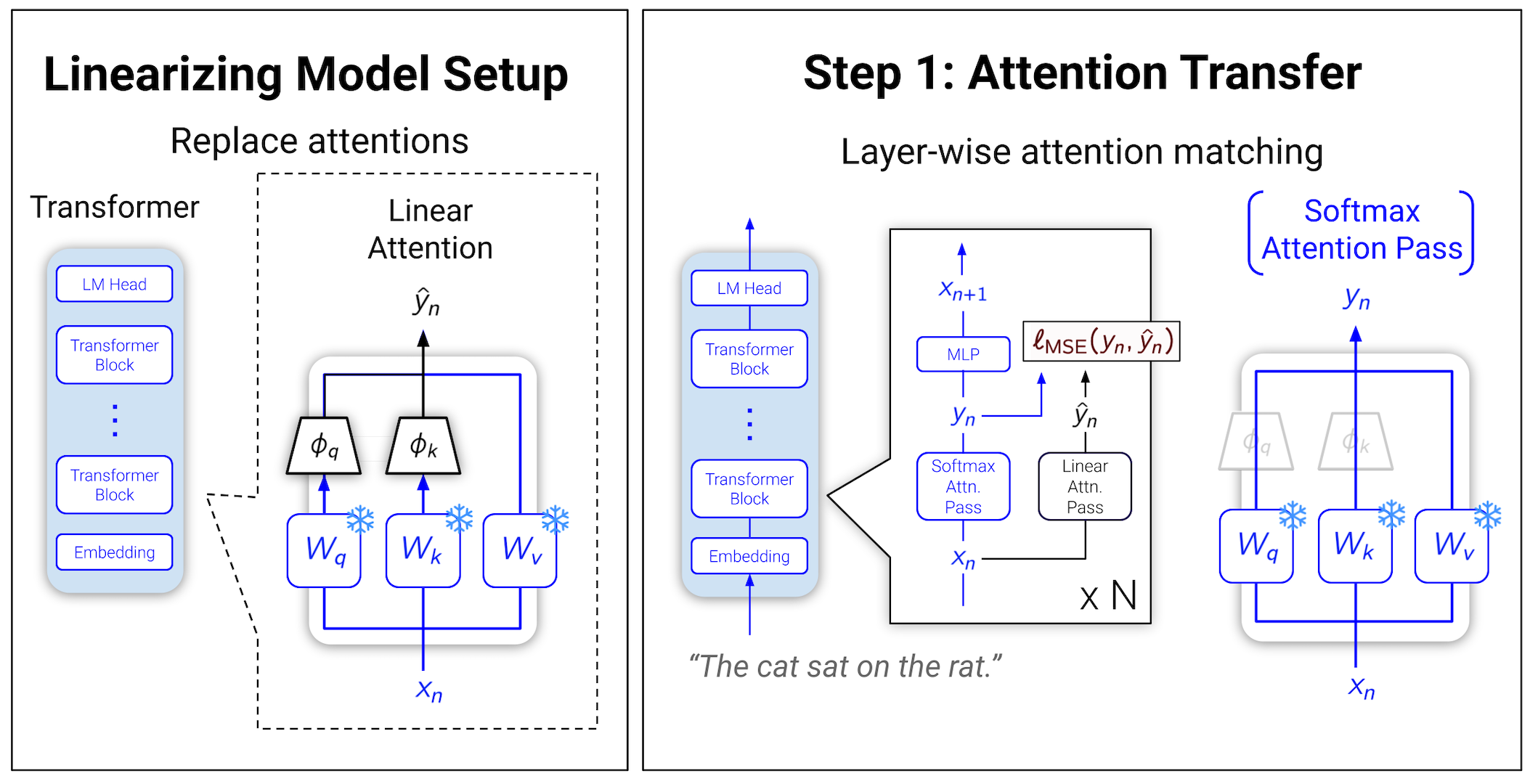
However, we found we could first simply train subquadratic attentions to mimic and replace softmax attention. This "attention transfer" was inspired by our earlier Hedgehog work. There, instead of manually designing linear attention feature maps $\phi$ to be good softmax approximators, we just set them as learnable layers. Surprisingly(?), we found we could explicitly train these layers to learn whatever functions were important to produce good softmax attention approximations.

This is the critical picture of what we're doing here. One linearized Llama 8B is just 32 hedgehogs trained in a trenchcoat.

For LoLCATs, we made two simple improvements to linearize LLMs:

1. While in Hedgehog, we only used learnable linear attentions, with LoLCATs we generalized to learnable linear-attention-and-sliding-window hybrids. This was inspired by our earlier Based work, where some local softmax attention helped improve quality. But now we unify the linear and softmax attentions in a single fully subquadratic layer. And train these layers to approximate softmax attention as whole. For an $N$-token sequence, the first $W$ tokens get softmax attention, the remaining $N-W$ get linear attention, and the values get combined as a learned weighted sum.

We support two sliding window implementations. (a) The usual implementation, and (b) a “terraced” window that exploits the ThunderKittens DSL’s primitives for fast CUDA kernels. Here we prefer contiguous blocks of size 64.

2. While in Hedgehog we trained the feature maps to match on attention weights (via a KL divergence), we found we could also use an MSE loss on the outputs of attention layers. This gets around a limitation of Hedgehog where we needed to instantiate all $N^2$ attention weights as "targets" to supervise. Instead, we can now use FlashAttention to compute softmax attention outputs, and keep attention transfer in $O(N)$ memory land.

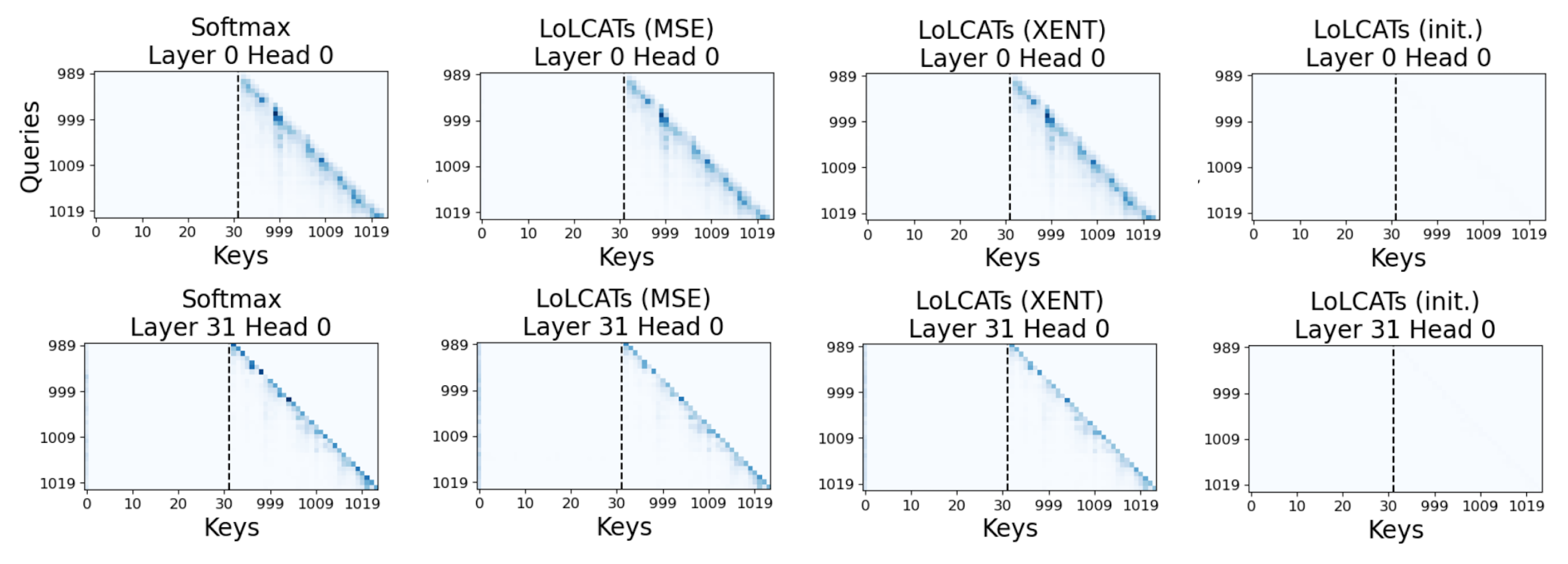
We really love our mathematical ways to approximate attention, but sometimes it pays off to just put our deep learning hats on. Like here, where we found we could simply learn how to approximate softmax with trainable linear attentions.

In all of the above, we create the linearized LLMs by simply inserting these feature maps into each existing attention. We only train these feature maps while freezing all other weights, amounting to just 0.2% of a 7B LLM's parameter counts.

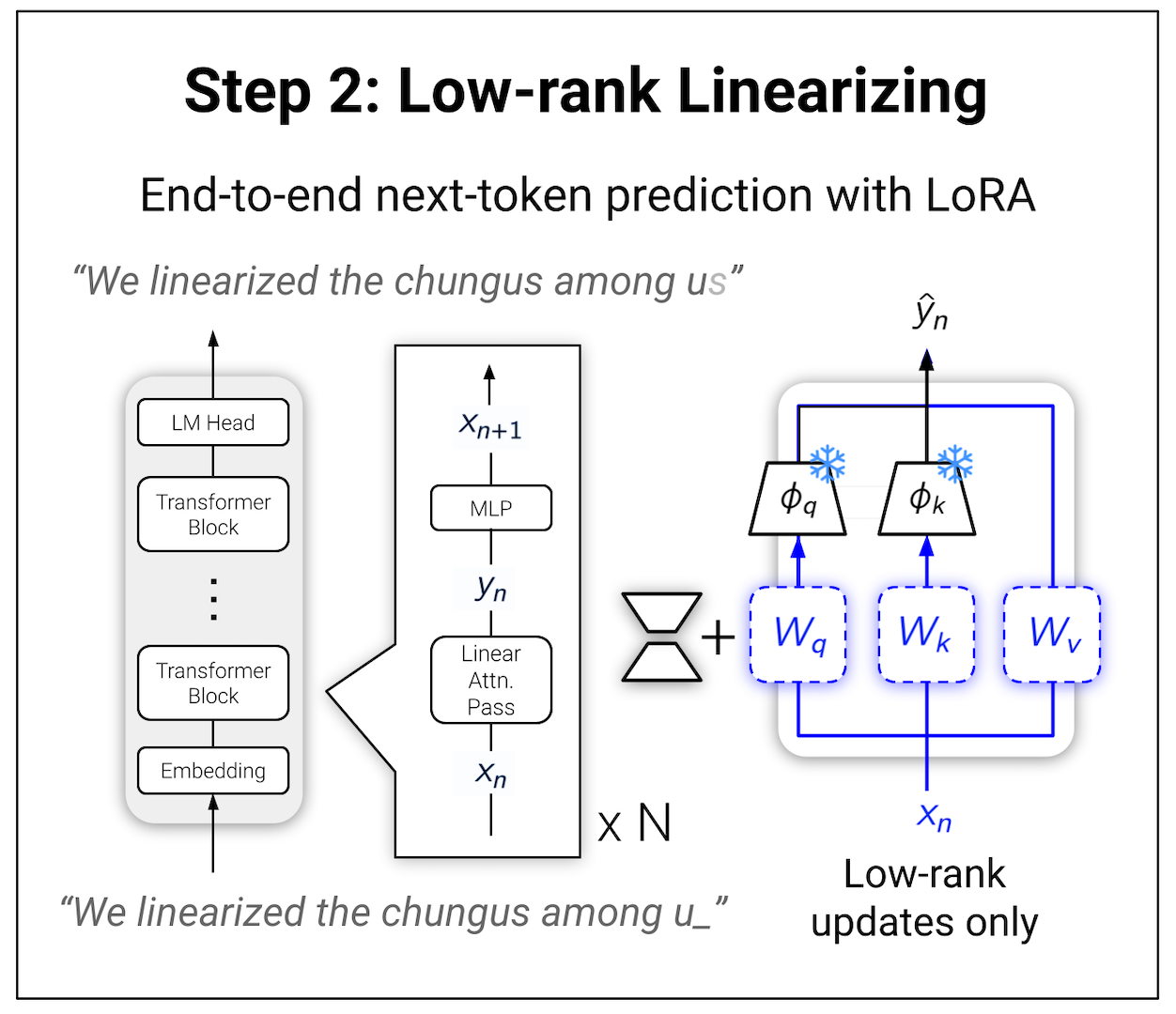
2. Low-rank Adaptation

With attention transfer we could train linear attentions to approximate softmax attentions. However, we still needed to do a bit more finetuning to "reconnect the wires" and get a coherent model. Fortunately, with LoLCATS we could do so by simply applying low-rank adaptation (LoRA) to attention QKVO weights. Keeping all else frozen, we train the LoRA weights so the LLM outputs minimize a next-token prediction loss over some natural language data. Then we’re done!

3. Layer-wise Optimization

At least for most cases. To help scale up LoLCATs to 405B LLMs, we had to add a third "L". While we could successfully linearize 7B+ and 70B LLMs by simply optimizing all layers jointly during attention transfer, this led to later layers having much higher attention MSEs than earlier ones. The larger MSEs escalated into a real problem for Llama 3.1 405B.

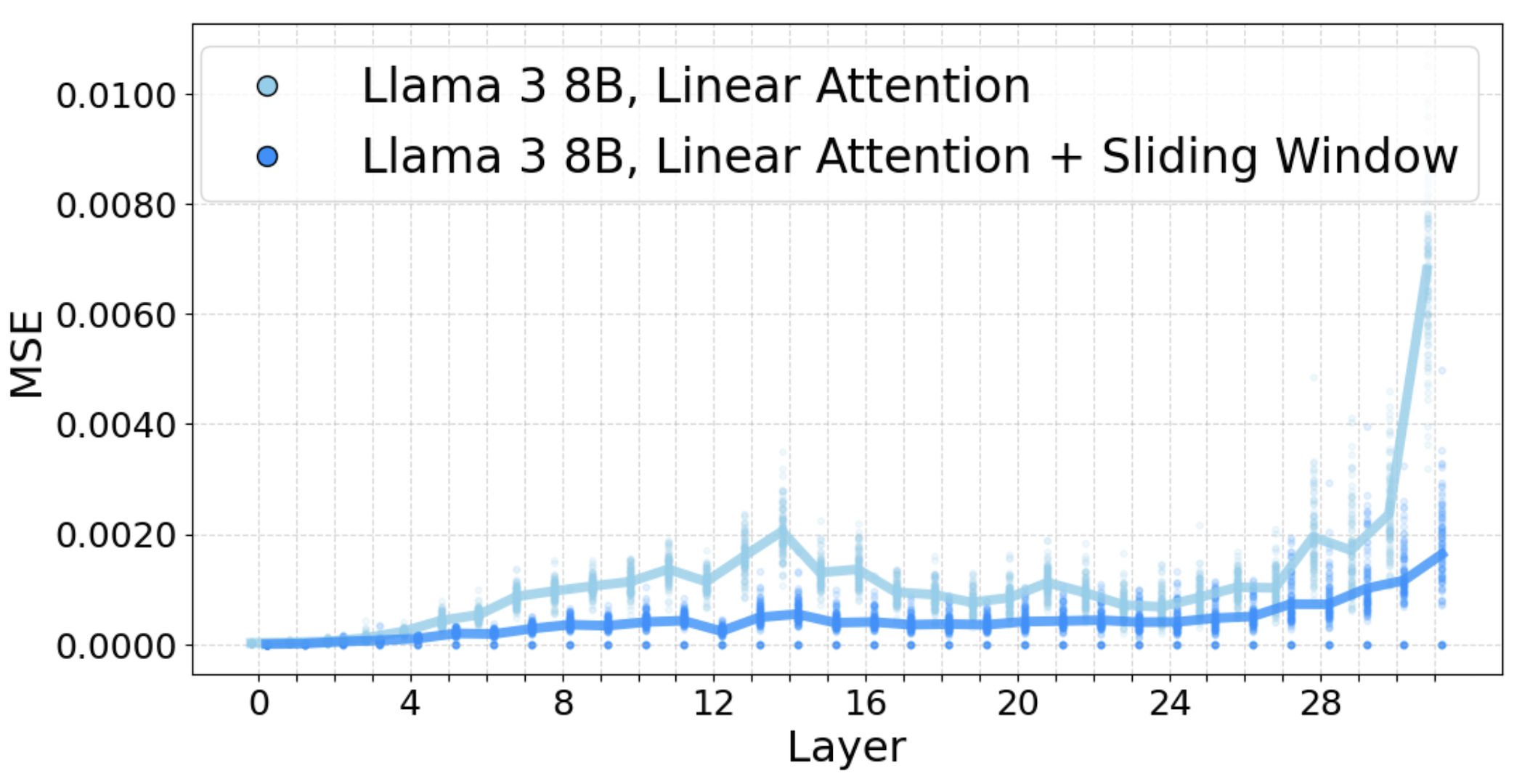
To resolve this and improve layer-wise attention transfer, we used a finer-grained "block-by-block" (or cria-by-cria ³) training setup. We split Llama 3.1 405B into blocks of $k$ layers and jointly trained the attentions only within each block. To train all blocks in parallel, with some linearizing data we simply precomputed LLM hidden states every $k$ layers, giving us the inputs for each block.

We pick $k$ to balance the speed of parallel training with the memory of precomputing and saving hidden states to disk. No fancy cost models here, but if we wanted to linearize with 50M tokens:

• At $k$ = 1, we’d need 2 bytes $\times$ 126 layers $\times$ 50M tokens $\times$ 16384 hidden size = 200TB of disk space to store the hidden states!
• At $k$ = 9, we cut this disk space down to just 22 TB, while still being able to train each 9-layer block on its own single GPU in parallel.

The latter sounded better to us. By splitting Llama 3.1 405B's 126 layers into 14 9-layer blocks, we could parallelize attention transfer on 14 different GPUs. This took just 5 hours. Then we stitched them all together with LoRA to get the final model.

---

Results

We now share some of our results, where LoLCATs improves the quality, training efficiency, and scalability of linearizing LLMs.

Closing the linearizing quality gap

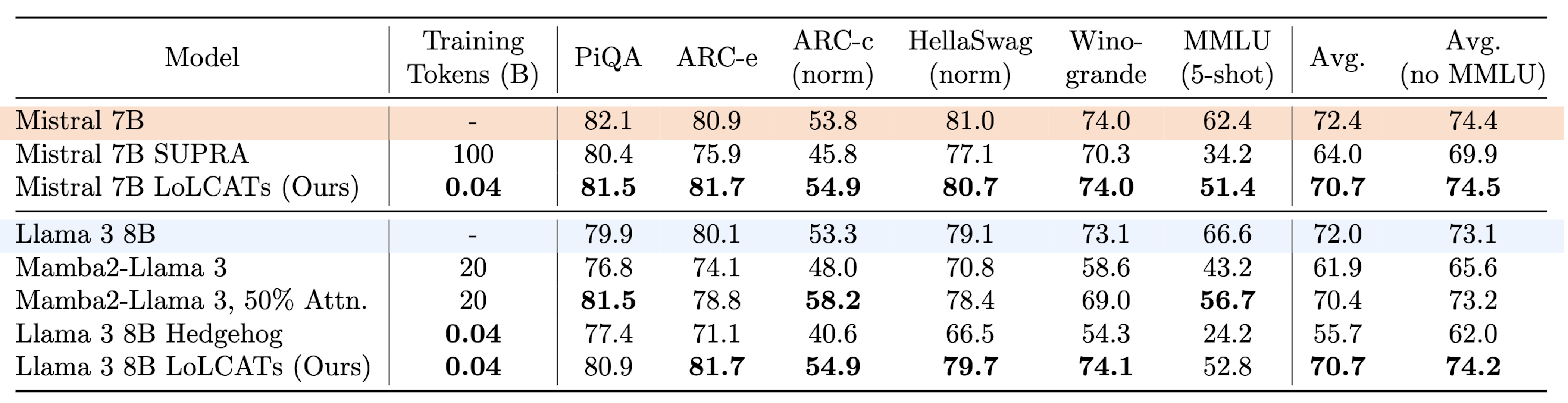
As a first test, we evaluated how LoLCATS compared to other linearizing methods at the popular 7B+ LLM scale. Across Mistral 7B v0.1 and Llama 3 8B LLMs, despite only training 0.2% of the model parameters on 40M tokens, LoLCATs closes $>$80% of the linearizing quality gap averaged across popular LM Evaluation Harness tasks. This outperforms concurrent methods needing 500 - 2500$\times$ the tokens. For the first time, LoLCATs further outperforms linearized hybrids with 50% of their layers being full softmax attention, while also closing the gap with the original 100% softmax attention Transformers on non-MMLU tasks.

Pushing linearized LLMs into state-of-the-art territory
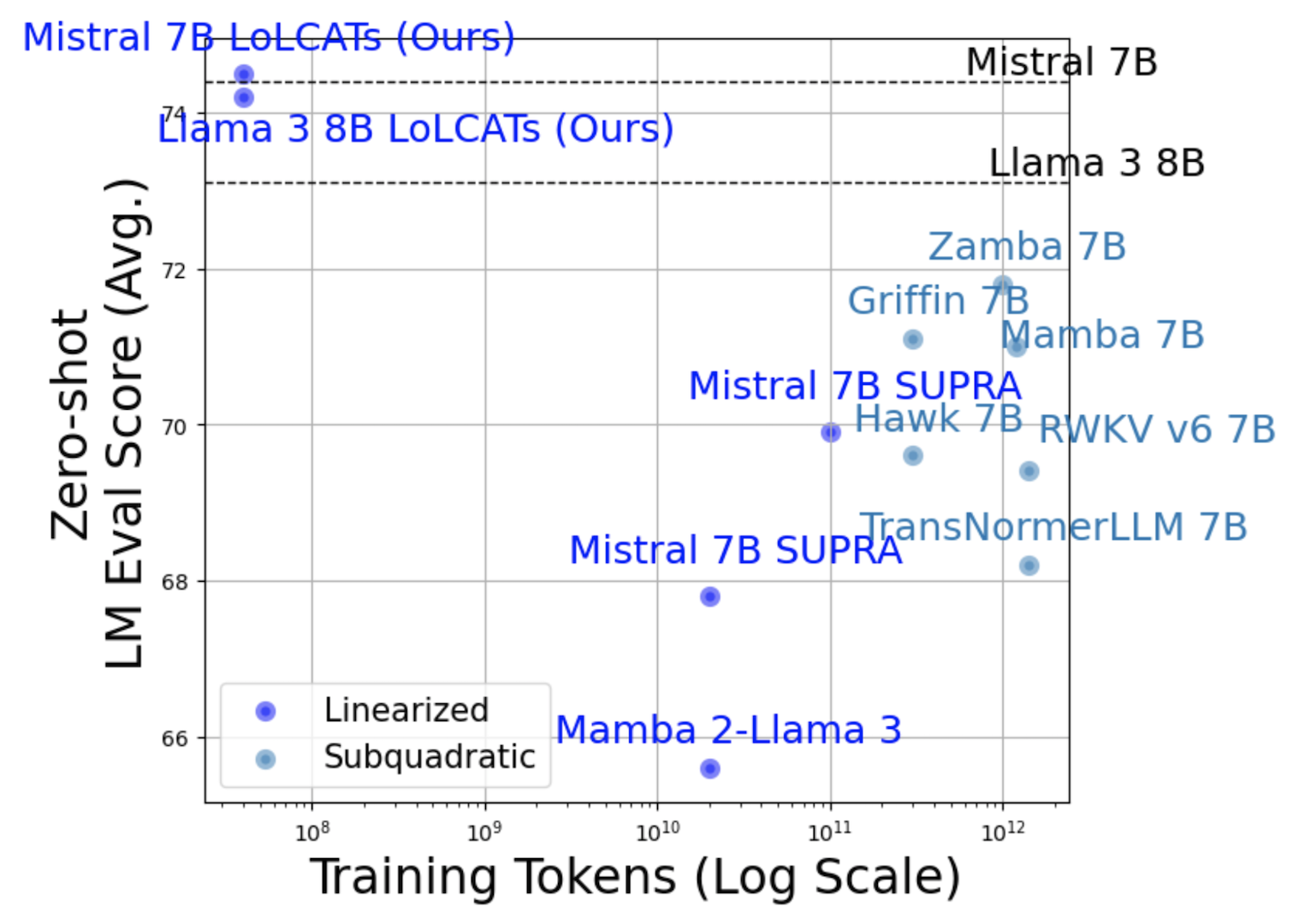
Along the way, we also found that LoLCATs could create state-of-the-art subquadratic LLMs in general. By converting available Transformers like Llama 3 8B or Mistral 7B, we created subquadratic LLMs that outperformed strong pretrained 7B Transformer alternatives by 1.2 to 9.9 higher LM Eval points (averaged over tasks). Furthermore, rather than pretrain on trillions of tokens, we got there with the same cost as a parameter-efficient finetune, using only 40M tokens no less (a 7,500 to 35,500$\times$ boost in "tokens-to-model" efficiency).

Drastically reducing linearizing costs

As alluded to above, with LoLCATs we could create state-of-the-art subquadratic LLMs with a fraction of prior training costs. Linearizing 7B and 8B LLMs required training just 0.2% of their model parameter counts on 40M tokens, doable in ~5 hours on a single 40GB A100. In our paper, we found that finding close softmax attention approximators was crucial to this efficiency boost. Across various prior linear attentions, by first training to approximate softmax attentions via attention transfer, we could rapidly speed up recovering linearized language modeling quality. We also found attention transfer alone wasn't enough. But fortunately only a few LoRA updates were all we needed to get the models talking!

Scaling up linearizing to 70B and 405B LLMs

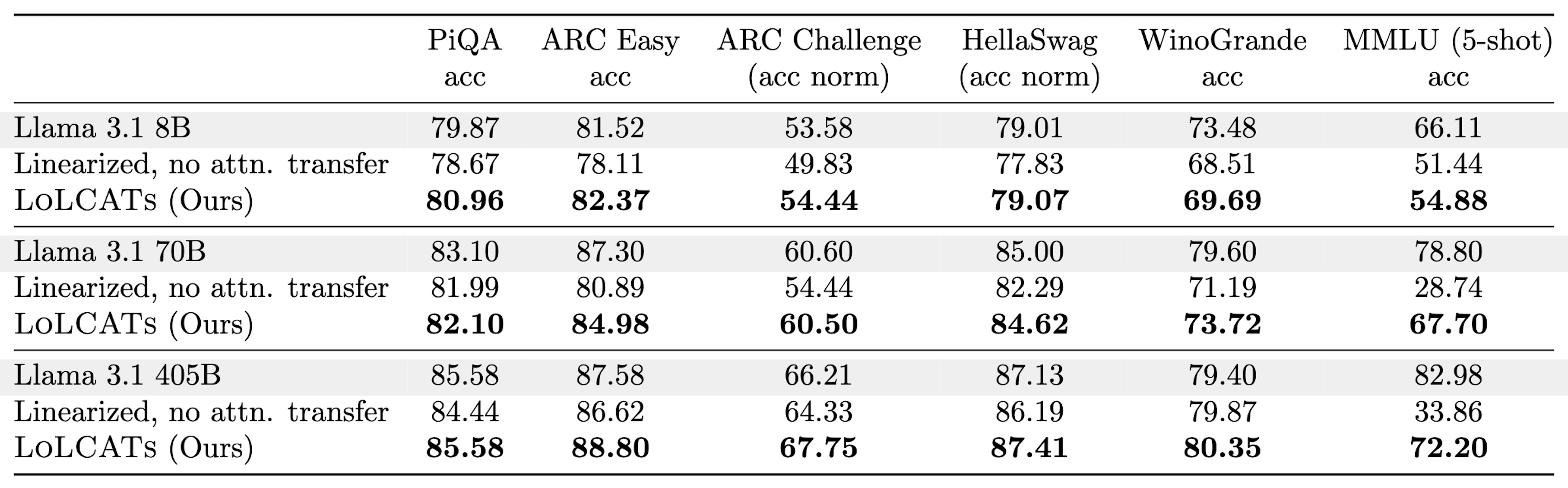
Finally, to really just see what these quality and training efficiency gains could do, we used LoLCATs to linearize the complete Llama 3.1 8B family. In the process, we created the first linearized 70B and 405B LLMs. Notably, linearizing Llama 3.1 70B took only 18 hours on a single 8x80GB H100. Linearizing Llama 3.1 405B still took less GPU hours than what prior methods used for 8B LLMs. LoLCATs also offers significant progress in quality, to tackle these big LLMs with reasonable compute. Compared with following the prior approach of just swapping attentions before training, we were able to close $>$78% of the performance gap to original Transformers on tasks like 5-shot MMLU.

---

What's next?

In summary, we made LoLCATs, a new method for linearizing LLMs with state-of-the-art quality and orders of magnitude less compute. While we’re excited to share our progress so far, we're also jazzed about the potential opportunities linearizing unlocks. Two such directions below:

Unlocking new capabilities with cheaper test-time compute

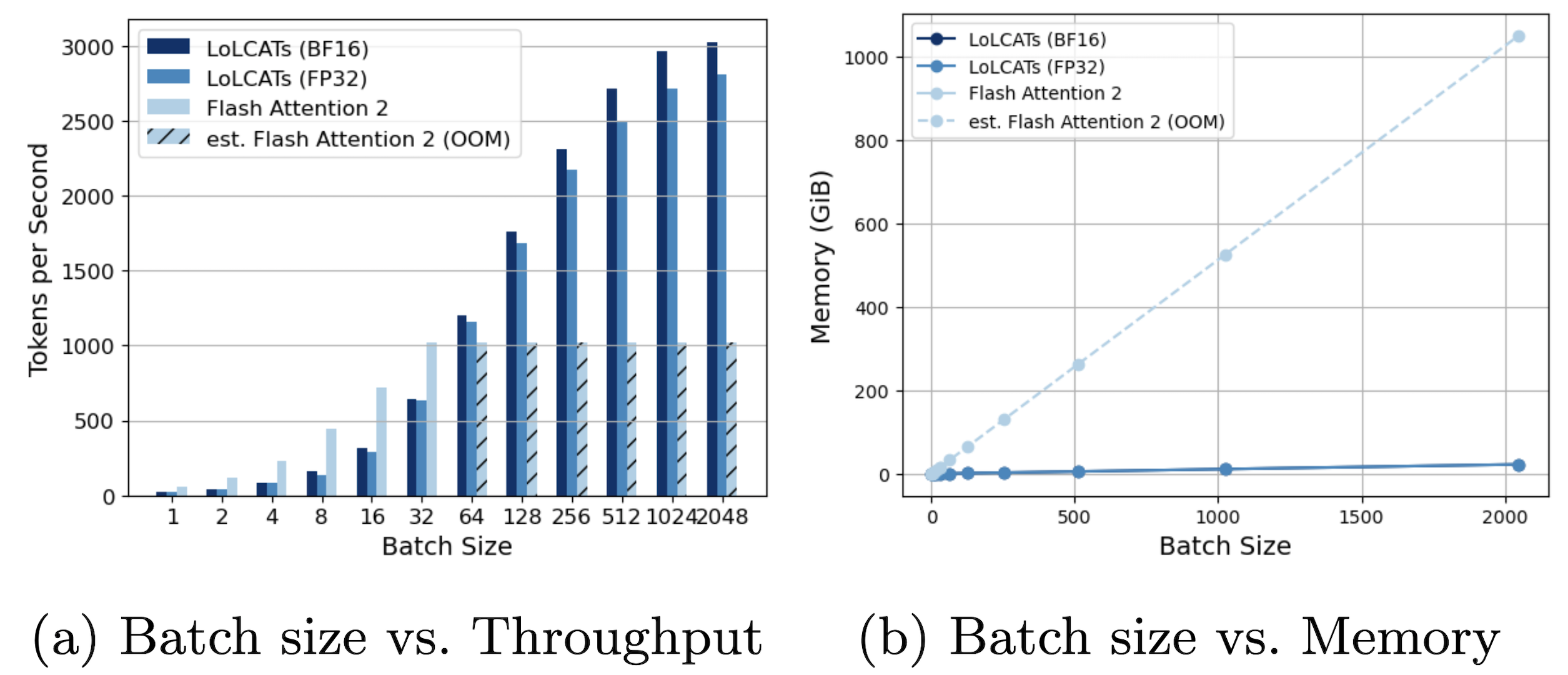
We're particularly excited about how linearizing LLMs lets us bring complexity-level improvements in efficiency---like linear-time and constant-memory generation---to readily-available and state-of-the-art LLMs. Our paper discusses this more, but by replacing each attention layer with a linear or recurrent alternative, we no longer need to deal with growing KV caches and their associated memory pains. Instead, we can dedicate that memory to more fun use-cases, such as achieving higher throughput with larger batch sizes.

Especially with recent attention on inference scaling laws---and improving answer quality by generating many responses---we're curious about further enabling these ideas, e.g., by now generating 2048 parallel responses at the prior cost of 32. By significantly bringing down the costs of test-time compute, could linearizing unlock further reasoning demonstrations and improve open-source model quality?

Democratizing Subquadratic LLM Development
We’re also excited about how low-rank linearizing can scale up efficient architecture research. While we stuck to simple linear attentions with LoLCATs, a big motivator was the ability to allow anyone to scale up a subquadratic candidate into competitive 7B+ LLMs that are all the rage these days. We've been fortunate that our RWKV, Gated Linear Attention, and Mamba friends (among others!) continue to cook up many exciting architectural developments—often on academic compute no less!

How can techniques like linearizing help take their ideas to bigger and badder models? While the effects might not be the same as pretraining from scratch, it seems like a great opportunity to use the open-weight ecosystem available today as a research testbed. Can we open up new avenues of efficient architecture development?

For both these pursuits, we’ve tried to make our training repo for LoLCATs helpful at https://github.com/HazyResearch/lolcats. Linearized Llamas for all!