Apr 19, 2022 · 6 min read
Advances in Understanding, Improving, and Applying Contrastive Learning
Dan Fu, Mayee Chen, Megan Leszczynski, and Chris Ré.
TL;DR: Contrastive learning has emerged as a powerful method for training ML models. In this series of three blog posts, we’ll discuss recent advances in understanding the mechanisms behind contrastive learning. We’ll see how we can use those insights to get better learned representations out of supervised contrastive learning, and see how we can apply contrastive learning to improve long-tailed entity retrieval.
Overview
Over the past few years, contrastive learning has emerged as a powerful method for training machine learning models. It has driven a revolution in learning visual representations, powering methods like SimCLR, CLIP, and DALL-E 2. The empirical success of these methods has begged the question – what makes contrastive learning so powerful? What is going on under the hood?
In this series of three blog posts, we’ll discuss recent advances in answering these questions.
- In part one (this blog), we’ll provide some background on contrastive learning and discuss some theoretical takes on how contrastive learning works.
- In part two, we’ll go over new developments on this understanding in the supervised setting, and show how to actually improve the representations produced by contrastive learning.
- In part three, we’ll see how we can use our understanding of contrastive learning to jump out of the visual domain—and improve the long-tailed performance of entity retrieval in NLP.
What is Contrastive Learning?
Contrastive learning describes a set of techniques for training deep networks by comparing and contrasting the models' representations of data. The central idea in contrastive learning is to take the representation of a point, and pull it closer to the representations of some points (called positives) while pushing it apart from the representations of other points (called negatives). The goal is to ensure that the representations themselves are meaningful, instead of just optimizing the models to generate a particular prediction.
For example, you might say that the representations of a dog and a crop of that dog, or representations of two dogs should be similar to each other. However, the representations of a dog and a cat (or a dog and an elephant) should be different from each other:
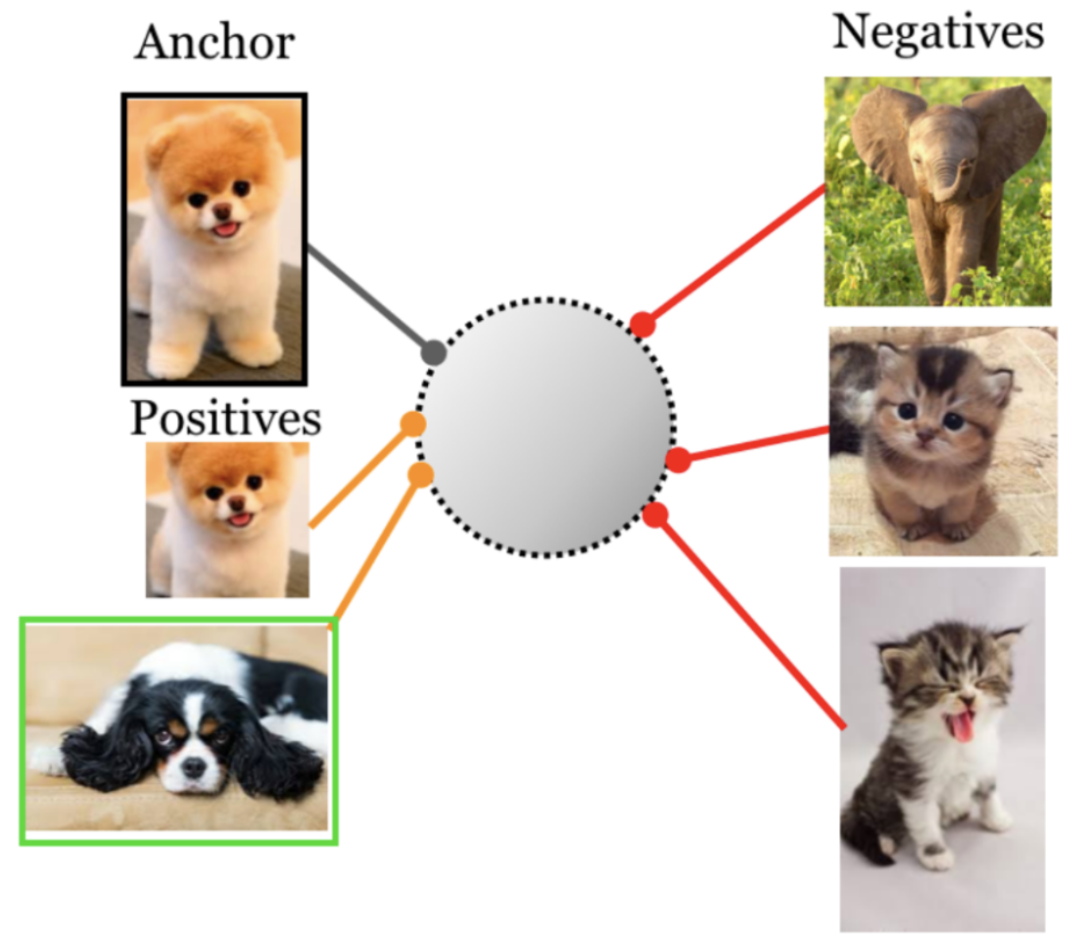
Figure 1. An example of (supervised) contrastive learning. The loss function says that the representations of the fluffy dog and the black and white dog should be close to each other, but far from the representations of the cats or the elephant. Source.
This runs in contrast (pun intended) to the traditional supervised learning paradigm, where machine learning models are just trained with a list of examples, with no relation to each other:

Figure 2. Traditional supervised learning. Models are trained with a list of labeled examples.
And it turns out that contrastive learning is a really good way to train high-performing models. The SimCLR paper demonstrated that it was possible for a self-supervised method to learn representations that match the performance of a supervised learning, and the SupCon paper showed that supervised contrastive learning (where positives are formed by class labels) might just be a better way to train models overall:
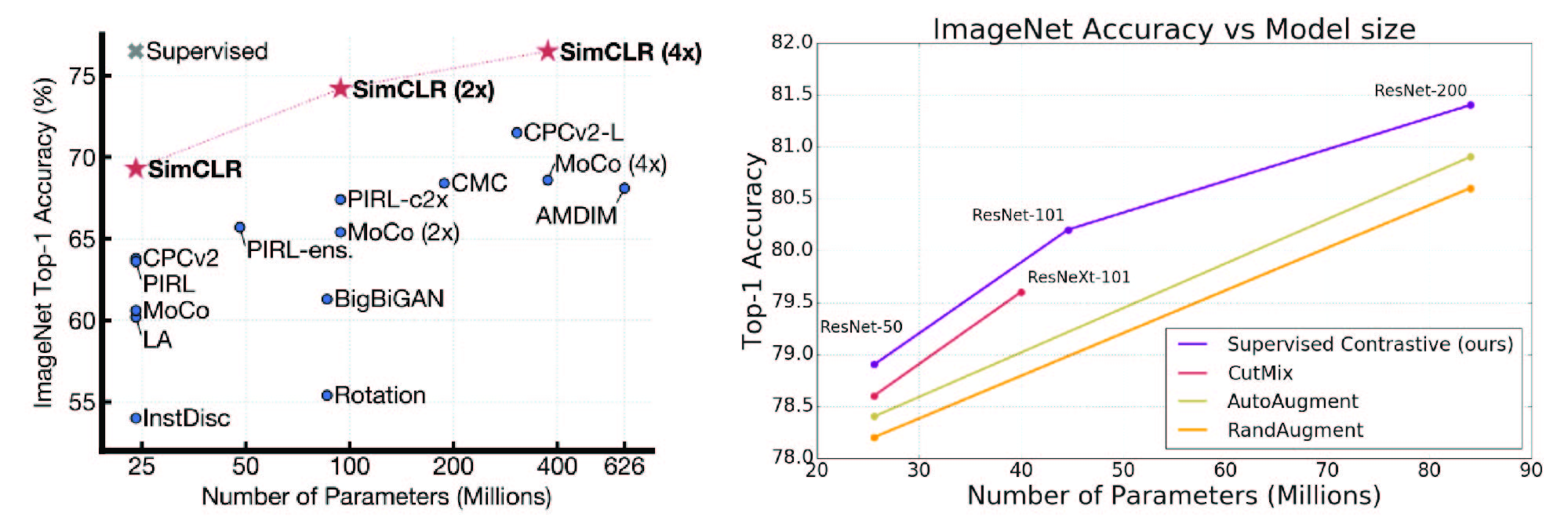
Figure 3. Left: SimCLR demonstrated that it was possible for a self-supervised model to match the performance of a fully-supervised model. Right: The SupCon paper showed that supervised contrastive learning might be a better way to train supervised models than traditional supervised learning. Sources: 1 2.
Why Does Contrastive Learning Work?
The strong empirical performance and wave of interest in these methods has led researchers to look into why contrastive learning works so well. In this section, we'll summarize some of these theoretical efforts and characterize them as falling into two camps. In part two of this blog series, we'll show how we can build upon these efforts to further improve the performance of supervised contrastive learning.
Geometric
These approaches characterize the geometry of the representations that get trained with contrastive learning. For example:
- Wang and Isola showed that there are two geometric forces at play in self-supervised contrastive learning: alignment and uniformity on the hypersphere (the n-dimensional sphere, i.e. when embeddings are normalized). Alignment encourages positive pairs (augmentations) to have the same representation, while uniformity encourages points to be as spread out as possible on the hypersphere.
- Graf et al looked at supervised contrastive learning, and showed that it asymptotically encourages class collapse – when every point from the same class has the same embedding—to a regular simplex with each class embedding maximally separated. This can explain why downstream classification performance is better with supervised contrastive learning; collapsed simplex embeddings are very easy to linearly separate.
- Robinson et al argue that properly sampling hard negatives, in contrast to uniform random sampling, is critical for a good geometry in the self-supervised setting. They introduce a family of sampling methods and show that certain conditions can lead to a similar class collapse.
Augmentations in Latent Subclasses
These approaches put augmentations front and center in their analysis, and argue that augmentations connect latent subclasses.
- Arora et al looked at the self-supervised setting and showed that reasoning about latent classes (e.g., the actual classes that you don't have labels for) can help explain why self-supervised contrastive learning performs well when evaluated on supervised tasks (as SimCLR was). In particular, it's possible to get good performance when a point and its augmentations define a class in the downstream supervised task.
- HaoChen et al relax the above condition and show that when points whose augmentations have some overlap define a downstream class (e.g., you can find a way to crop two different dogs to roughly the same image), self-supervised contrastive losses can learn representations that perform well.
These theoretical advances have done wonders for our understanding of how contrastive learning works. In part 2 of this blog series, we’ll talk about how we build on both these lines of work to improve the transfer and robustness of supervised contrastive learning, where we find that understanding both the geometry as well as the role of data augmentation and other inductive biases is critical for characterizing representation quality.
What's Next
Check out parts 2 and 3 of this blog series to see how we build on these previous insights to improve supervised contrastive learning and entity retrieval!