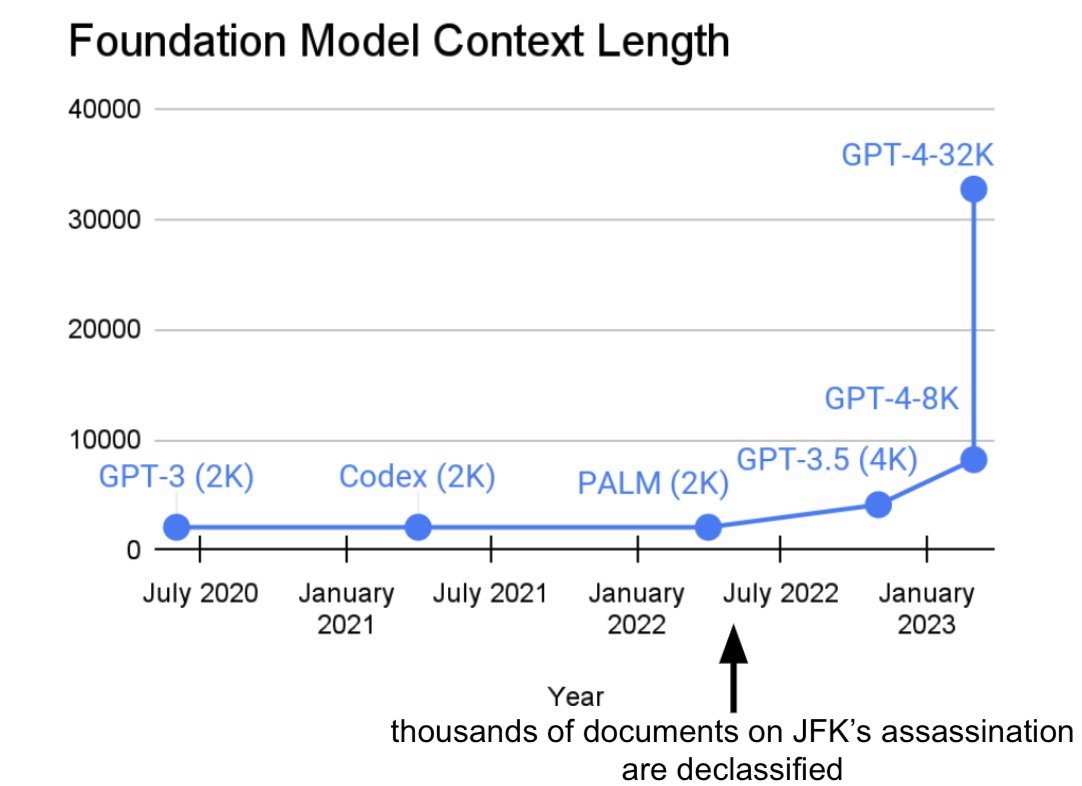
For the last two years, a line of work in our lab has been to increase sequence length. We thought longer sequences would enable a new era of machine learning foundation models: they could learn from longer contexts, multiple media sources, complex demonstrations, and more. All data ready and waiting to be learned from in the world! It’s been amazing to see the progress there. As an aside, we’re happy to play a role with the introduction of FlashAttention (code, blog, paper) by Tri Dao and Dan Fu from our lab, who showed that sequence lengths of 32k are possible–and now widely available in this era of foundation models (and we’ve heard OpenAI, Microsoft, NVIDIA, and others use it for their models too–awesome!).
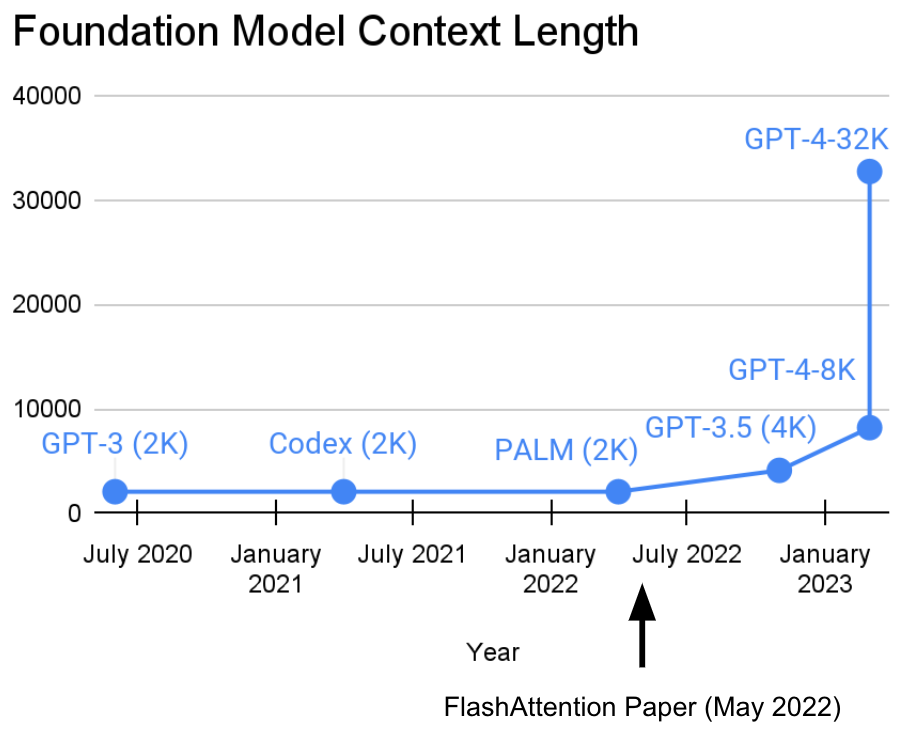
The context lengths of foundation models have been growing recently (and alternate explanations abound)! What's next?
As the GPT4 press release noted, this has allowed almost 50 pages of text as context–and tokenization/patching ideas like those in Deepmind’s Gato are able to use images as context. So many amazing ideas coming together, awesome!
This article is about another approach to increasing sequence length at a high level, and the connection to a new set of primitives.
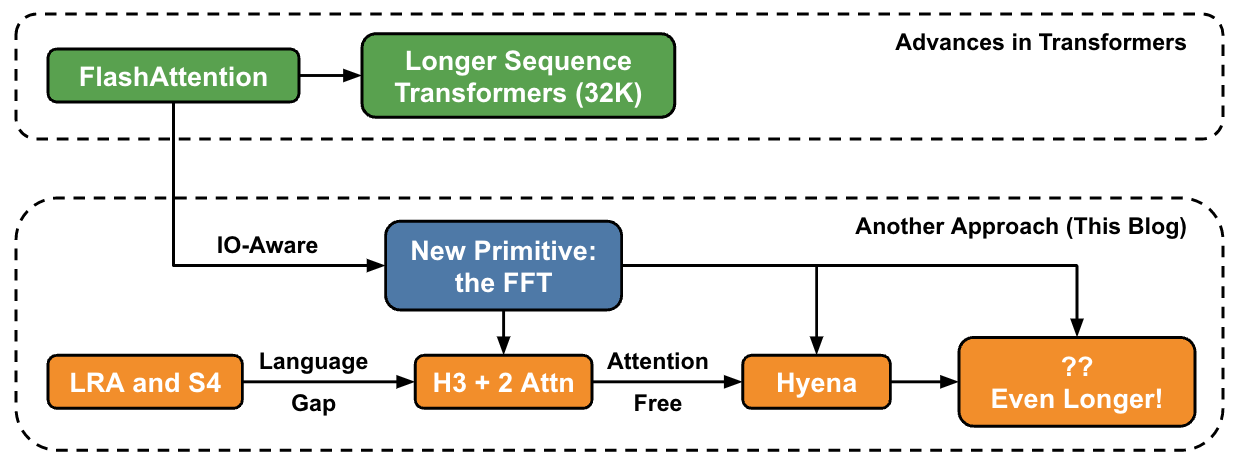
This blog is about another approach to increasing sequence length!
One fundamental issue we ran into was that the attention layers in Transformers scale quadratically in sequence length: going from 32k length to 64k length isn’t 2x as expensive, but 4x more expensive. This led us to investigate models that are nearly linear time in sequence length. For our lab, this started with Hippo, followed by S4, H3, and now Hyena. These models hold the promise to have context lengths of millions… or maybe even a billion!
Some Recent History and Progress
Long Range Arena and S4
The Long Range Arena benchmark was introduced by Google researchers in 2020 to evaluate how well different models can handle long-range dependencies. LRA tests a suite of tasks covering different data types and modalities such as text, images, and mathematical expressions, with sequence lengths up to 16K (Path-X: classifying images that have been unrolled into pixels, without any spatial inductive bias). There’s been a lot of great work on scaling Transformers to longer sequences, but many of them seem to sacrifice accuracy. And there’s that pesky Path-X column: all these Transformer methods and their variants struggled to do better than random guessing.
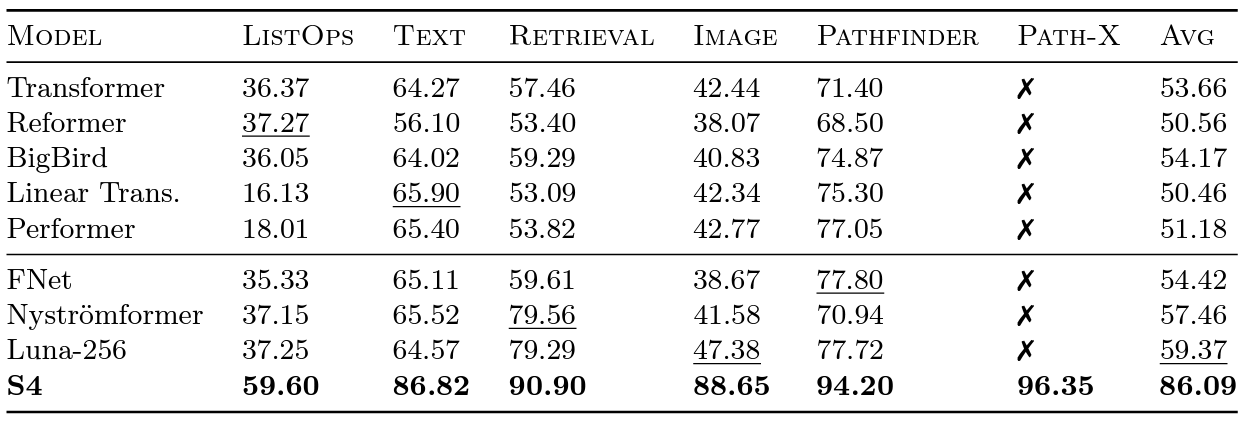
Transformer variants benchmarked on Long Range Arena, along with S4.
Enter S4, led by the amazing Albert Gu! Inspired by the results from the LRA benchmark, Albert wanted to figure out how to better model long-range dependencies. Building on a long line of work on orthogonal polynomials and the relationships between recurrent and convolutional models, we introduced S4 – a new sequence model based on structured state space models (SSMs).
Critically, SSMs scale with in sequence length , instead of quadratically like attention. S4 was able to successfully model the long-range dependencies in LRA, and was also the first model to achieve better than average performance on Path-X (and can now get 96.4% accuracy!). Since releasing S4, we’ve been super excited by how people are building on the ideas and making the space richer: with models like S5 from Scott Linderman’s group, DSS from Ankit Gupta (and our own follow-on collaboration S4D), Liquid-S4 from Hasani & Lechner, and more – and of course we are always indebted to Sasha Rush and Sidd Karamcheti for the amazing Annotated S4!
As an aside: when we released FlashAttention, we were able to increase the sequence length of Transformers. We found that Transformers could also get non-trivial performance (63%) on Path-X – simply by increasing the sequence length to 16K!
The Gap with Language
But S4 still had a gap in quality on language modeling – up to 5 perplexity points (for context, that’s the gap between a 125M model and a 6.7B model). To close this gap, we looked at synthetic languages like associative recall to figure out what properties you should need for language. We ended up designing H3 (Hungry Hungry Hippos) – a new layer that stacked two SSMs, and multiplied their outputs together with a multiplicative gate.
Using H3, we replaced almost all the attention layers in GPT-style Transformers, and were able to match Transformers on both perplexity and downstream evaluations, when trained on 400B tokens from the Pile:
| Model | Pile PPL | SuperGlue Zero-Shot |
|---|---|---|
| GPT-Neo-1.3B | 6.2 | 52.1 |
| H3, 2 attn (1.3B) | 6.0 | 56.5 |
| GPT-Neo-2.7B | 5.7 | 54.6 |
| H3, 2 attn (2.7B) | 5.4 | 56.8 |
Since the H3 layer is built on SSMs, it also has compute that grows in in sequence length. The two attention layers still make the whole model overall, but more on that in a bit...
Of course, we weren’t the only folks thinking in this direction: GSS also found that SSMs with gating could work well in concert with attention in language modeling (which inspired H3), Meta released their Mega model which also combined an SSM with attention, the BiGS model replaced attention in BERT-style models, and our RWKV friends have been looking at completely recurrent approaches. Very exciting work in this area!
The Next Advance: Hyena
The next architecture in this line of work is Hyena – we wanted to see if it was possible to get rid of those last two attention layers in H3, and get a model that grows nearly linearly in sequence length. Turns out, two simple insights led us to the answer:
- Every SSM can be viewed as a convolution filter the length of the input sequence – so we can replace the SSM with a convolution the size of the input sequence, to get a strictly more powerful model for the same compute. In particular, we parametrize the convolutional filters implicitly via another small neural network, borrowing powerful methods from the neural fields literature, and the great CKConv / FlexConv line of work. Plus, the convolution can be computed in time in sequence length – nearly-linear scaling!
- The gating behavior in H3 can be generalized: H3 takes three projections of the input, and iteratively takes convolutions and applies a gate. In Hyena, we simply add more projections and more gates, which helps generalize to more expressive architectures and closes the gap to attention.
In Hyena, we proposed the first fully near linear-time convolutional models that could match Transformers on perplexity and downstream tasks, with promising results in initial scaling experiments. We trained small- and medium-sized models on subsets of the PILE, and saw that val PPL matched Transformers:
| Model | 5B | 10B | 15B |
|---|---|---|---|
| GPT-2 Small (125M) | 13.3 | 11.9 | 11.2 |
| Pure H3 (153M) | 14.8 | 13.5 | 12.3 |
| Hyena (153M) | 13.1 | 11.8 | 11.1 |
| GPT-2 Medium (355M) | 11.4 | 9.8 | 9.3 |
| Hyena (355M) | 11.3 | 9.8 | 9.2 |
With some optimizations (more on that below), Hyena models are slightly slower than Transformers of the same size at sequence length 2K – but get a lot faster at longer sequence lengths.
We’re super excited to see how far we can take these models, and excited to scale them up to the full size of the PILE (400B tokens): what happens if we combine the best ideas from H3 and Hyena, and how long can we go?
A Common Primitive: the FFT... or Something More Basic?
A common primitive in all these models is the FFT – that’s how we can efficiently compute a convolution as long as the input sequence in time. However, the FFT is poorly supported on modern hardware, which is dominated by specialized matrix multiplication units and GEMMs (e.g., tensor cores on NVIDIA GPUs).
We can start to close the efficiency gap by rewriting the FFT as a series of matrix multiplication operations – using a connection to Butterfly matrices that folks in our group have used to explore sparse training. In our recent work, we’ve used this connection to build fast convolution algorithms like FlashConv and FlashButterfly, by using a Butterfly decomposition to compute the FFT as a series of matmul operations.
But we can draw on the prior work to make a deeper connection: you can also let these matrices be learned – which takes the same wall-clock time, but gives you extra parameters! We’ve started exploring this connection on some small datasets with promising initial results, and we’re excited to see where else this connection can take us (how can we make it work for language models?):
| Block Size | sCIFAR Acc |
|---|---|
| Baseline | 91.0 |
| 16x16 Learned | 91.8 |
| 32x32 Learned | 92.4 |
| 256x256 Learned | 92.5 |
We’re looking forward to exploring this more deeply. What class of transforms does this extension learn, and what can it allow you to do? What happens when we apply it to language?
What's Next
We are super excited by these directions, and what’s next: longer and longer sequences, new architectures that allow us to explore this new regime. We’re especially motivated by applications that could benefit from longer-sequence models – high-resolution imaging, new modalities of data, language models that can read entire books. Imagine giving a language model an entire book and having it summarize the plot, or conditioning a code generation model on all the code you’ve ever written. The possibilities are wild – and we’re excited.
You can find model code to play around with the synthetics languages we used to develop H3 & Hyena here. If you’re also excited by these directions, please reach out – we would love to chat!
Dan Fu: danfu@cs.stanford.edu; Michael Poli: poli@stanford.edu
Acknowledgements
Thanks to Alex Tamkin, Percy Liang, Albert Gu, Michael Zhang, Eric Nguyen, and Elliot Epstein for their comments and feedback on this post.
Alternate Explanations Abound
H/t to @typedfemale for bringing this to our attention. ↩