Aug 12, 2023 · 7 min read
Embroid: Correcting and Improving LLM Predictions Without Labels
Neel Guha*, Mayee F. Chen*, Kush Bhatia*, Azalia Mirhoseini, Chris Ré.
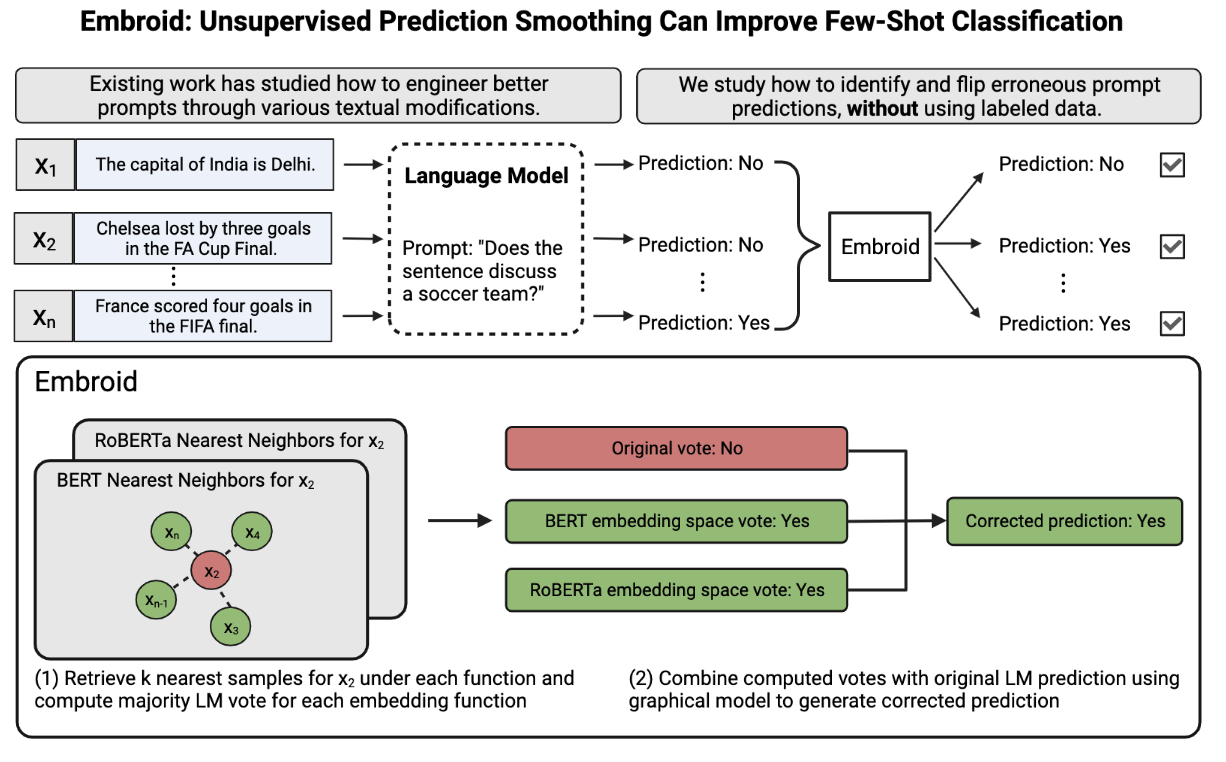
This blogpost describes our recent work on improving the performance of prompted language models without labeled data. Specifically, we leverage the observation that because the embedding spaces of models like BERT are smooth with respect to task labels, enforcing agreement between a prompt's prediction on a sample and the predictions on the nearest neighbors of improves prompt accuracy over the entire dataset. The full paper can be found here, and corresponding code here.
Motivation
In many domains, a significant barrier to valuable empirical analysis is the need to manually annotate data, and the cost of doing so. For instance, a legal analyst attempting to count the number of contractual clauses (from a database) which contain audit rights1 would have to manually label all candidate clauses. Thus, recent works have begun exploring if language models (LMs) could replace manual labeling at scale. The appeal of these models is that because they can be transformed into classifiers via prompts, domain experts need only spend time writing the prompt. As the resource requirements for running these models (in compute and time) continue to decline, they become an increasingly cheap alternative to hand-annotation. Returning to the example above, our legal analyst could---instead of manually labeling---use a model like GPT-4 to classify whether or not a clause creates an audit right (see below).
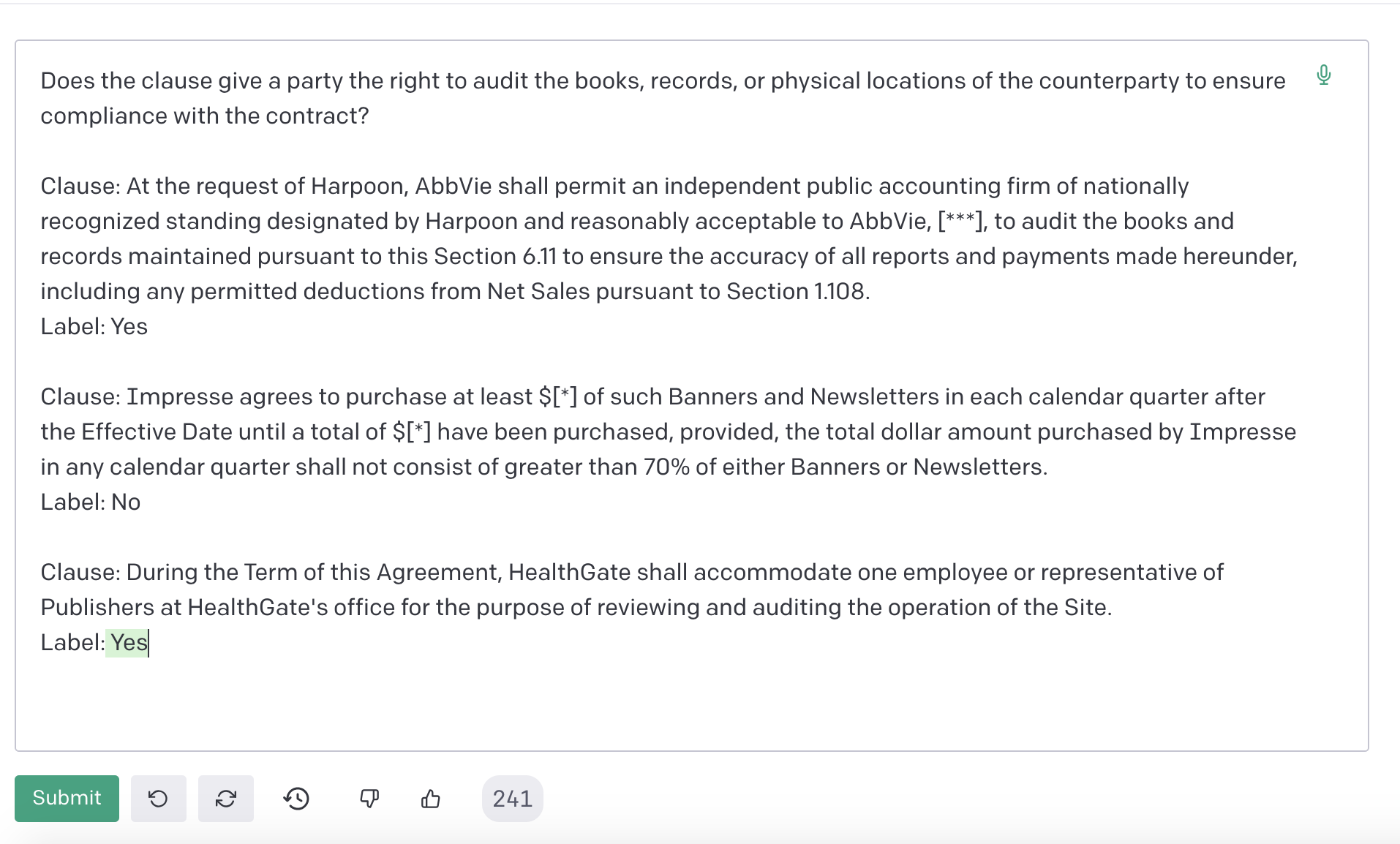
Figure 1: Using GPT-3.5 to classify whether a candidate clause creates an audit right. GPT-3.5's prediction is correct.
Unfortunately, the process of writing prompts ("prompt engineering") is something of a dark art. Because small changes to a prompt can alter performance, the most common approach for designing prompts is to assemble a large collection of validation data, and manually evaluate different prompt formats. The problem, of course, is that collecting this type of validation data is infeasible for the reasons described above.
In recent work, we explored whether it was possible to improve the quality of a prompt's predictions without needing labeled data. In other words: are there strategies that data scientists working in label-limited regimes could employ to improve the few-shot performance of LMs?
Embroid: Using Old-School Embeddings to Improve Performance
Prior work has found that the embedding spaces of BERT-like models are smooth with respect to different tasks. Here, smoothness means that samples which are "close-by" in embedding space have the same label for a given task. The exciting observation for BERT models is that their embedding spaces are smooth for a wide range of tasks---everything from sentiment detection to classifying legal contractual clauses. Thus, past efforts have explored how smoothness can be used to make predictions for unlabeled samples by using their proximity to known labeled samples.2
Embroid inverts this observation: rather than using the smoothness to propagate predictions to unlabeled samples, we can use use smoothness to check the correctness of LM predictions. The intuition is that LMs often make mistakes in unpredictable ways, and small modifications to the text of an input can alter the prediction generated (see below for an example, and HELM for a more comprehensive description of this phenomenon).
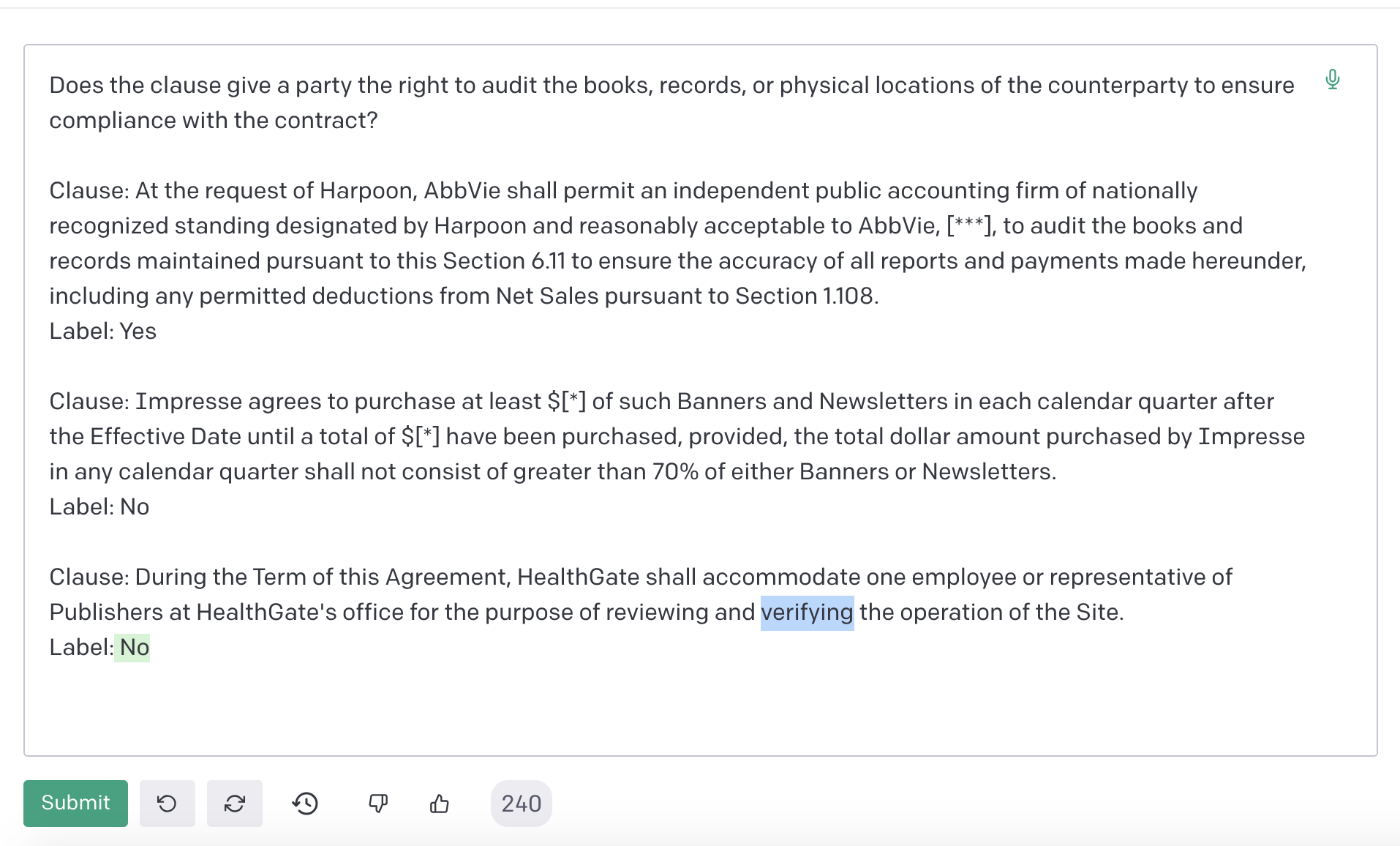
Figure 2: A small perturbation to the language of the clause in the example above (i.e., ) does not change its meaning, but leads GPT-3.5 to alter its prediction.
Specifically, the smoothness property dictates that a neighborhood of samples which clustered tightly together should all share the same true label. Thus, if an LM's prediction for one of those samples differs from the LM's prediction for most neighbors, the disagreeing prediction is likely wrong. By identifying samples for which LM predictions disagree with the predictions assigned to neighbors, we can identify instances where an LM is mispredicting. And by adjusting these predictions to match those of their neighbors, we can actually improve prediction accuracy overall.
Avoiding Overreliance on a Single Embedding Space
But what if the LM prediction isn't actually wrong, and the embedding space is unhelpful (e.g., it places samples from different classes next to each other)? How do we know when prediction disagreement is actually due to mispredictions, and not just error in the embedding space?
To get around this problem, we perform the neighborhood comparisons in embedding spaces from multiple different models (e.g., RoBERTa, SentenceBERT, BERT, LegalBERT, etc.). We find that different embedding spaces surface different relationships between samples. Though two models may generate embedding spaces which are equally smooth, an instance's nearest neighbors will differ across the embedding spaces. The lack of correlation across embedding spaces means that analyzing a sample's neighborhood in each embedding space provides a more robust picture of whether an LM's prediction is incorrect.
The intuition behind Embroid is that for each instance , we can use each embedding space to generate an additional prediction for . Given embedding spaces, we can combine these predictions with the original LM prediction using weak supervision. For those less familiar: weak supervision allows us to combine the predictions of multiple noisy voters into a single final prediction, without labeled data. The advantage of weak supervision is that it's sensitive to the fact that different voters may have different overall accuracies, and implicitly learns accuracy-weights for each source. Thus, a single voter being considerably worse than the others should not jeopardize performance. Mechanically, weak supervision casts the problem of estimating the prediction as inference over a latent variable graphical model. We rely on a particular method called Flying Squid, which has the added benefit of being both fast and accurate.
How do we generate a prediction from each embedding space? For an embedding space , we identify the nearest neighbors for using 's embeddings. We then compare the class balance of the LM's predictions in the neighborhod to the class-balance of the LM's predictions over the entire dataset. The neighborhood vote generated is the class for which the neighborhood is more dense than the global dataset. For example, if the LM predicts class +1 30% of the time for the entire dataset, but 40% of the time for 's neighbors, then the prediction generated for would be +1.
Something nice is that weak supervision's formal mathematical grounding allows us to theoretically analyze Embroid. In Section 5 of our paper, we characterize different factors which drive Embroid's performance, including the smoothness of the embedding space and the accuracy of the original prompt's predictions.
Results
We encourage you to read the full paper to learn more about our experiments. The quick highlights are:
- On a wide-ranging study of 95 different tasks (spanning different domains), we find that Embroid consistently improves the original prompt predictions. On GPT-JT, for instance, Embroid improves 89.1% of the time, by an overall average of 7.3 F1 points. These improvements extend to API-access models as well. Our study (on a smaller subset of tasks) shows that Embroid improves GPT-3.5 almost 81% of the time, by an average of 4.9 F1 points.
- Because Embroid is agnostic to the prompt text, it can be combined with different prompting strategies. We find that it improves performance when performed in conjunction with AMA, chain-of-thought, and demonstration-selection engineering strategies.
- Finally, Embroid can be customized to domains via the embedding models that are chosen. We find, for instance, that choosing legal embedding models (available on HuggingFace!) improves general domain LMs for legal tasks.
Acknowledgements
We thank Gautam Machiraju and other members of the Hazy Research Group for feedback on this post.
- An "audit right" is the right for one party to the contract to audit the counterparty to ensure compliance with the contract. This could involve inspecting books or premises. Examples of contractual clauses containing audit rights can be found here.↩
- In addition to Liger, recent work on label propagation has exploited this observation.↩