ThunderKittens: Bringing fp8 to theaters near you

Repo: https://github.com/HazyResearch/ThunderKittens
With team: Benjamin Spector, Aaryan Singhal, Daniel Y. Fu, Chris Ré

Feature update! We’ve gotten a lot of requests for supporting quantized data types in ThunderKittens. Today, we’re happy to bring you fp8 support and fp8 kernels! This post dives into our approach.

fp8 gemm

1500 TFLOPS in 95 lines of code. Checkout our kernel here, make && ./matmul!

implementation details

The main goal for TK, has always been to make it easier to write kernels for and do research on new architectures. That being said, there are key differences across the data types (fp8, fp16, ...) that could make things messy. Rather than versioning our TK library functions for each data type and requiring developers to think about each data type differently when programming, we want to find a way of incorporating fp8, while maintaining a simple, unified programming experience. For those of you who are interested in learning a bit about our approach to implementing fp8 support, let’s dive in!

Refresher on TK’s tile data structure: The most basic data structure in TK is a $16\times16$ tile. We have tiles for both shared and register memory. Our primary goal, given TK’s focus on supporting AI use cases, is to make the tile compatible with tensor core instructions. A tensor core executes GEMMs. A GEMM (matrix-multiply accumulate, MMA) is:

for accumulator matrix $D$, and input matrices $A$ (row-major), $B$ (column-major), and $C$ (row-major). Typically, $D$ is in a higher precision, like fp32 or fp16.

launching warp-level gemms

Let's start with the basic MMA instruction, where warps / groups of 32 threads execute GEMMs on matrices held in register memory. The GPU instruction expects particular layouts for matrices $A, B, C,$ and $D$. For instance:

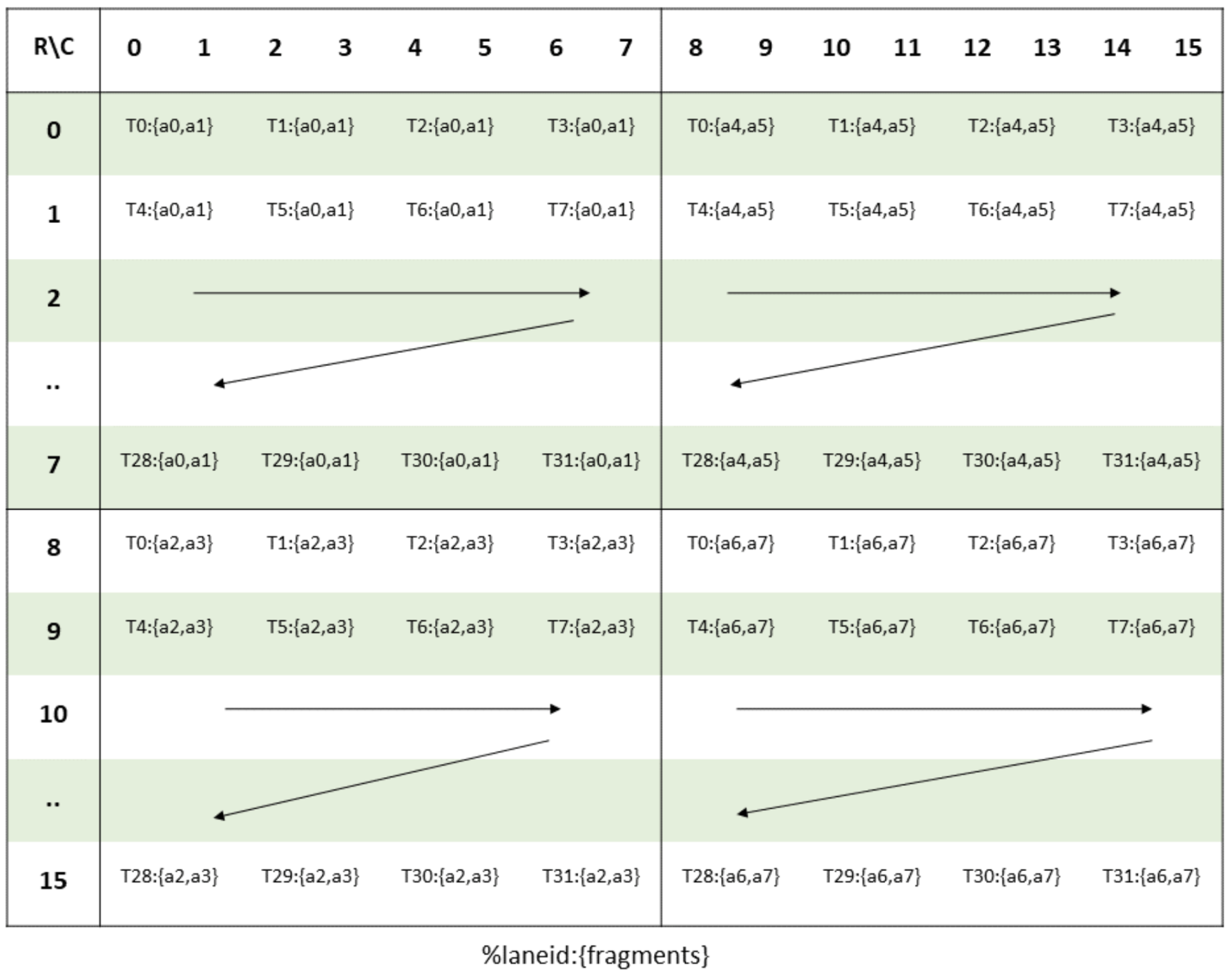
Thread ownership over fp16 and bf16 elements in register memory for input matrix $A$ would look as follows. $Ti$ indicates thread $i$'s ownership, and the row / column numbers index into the elements of the matrix.

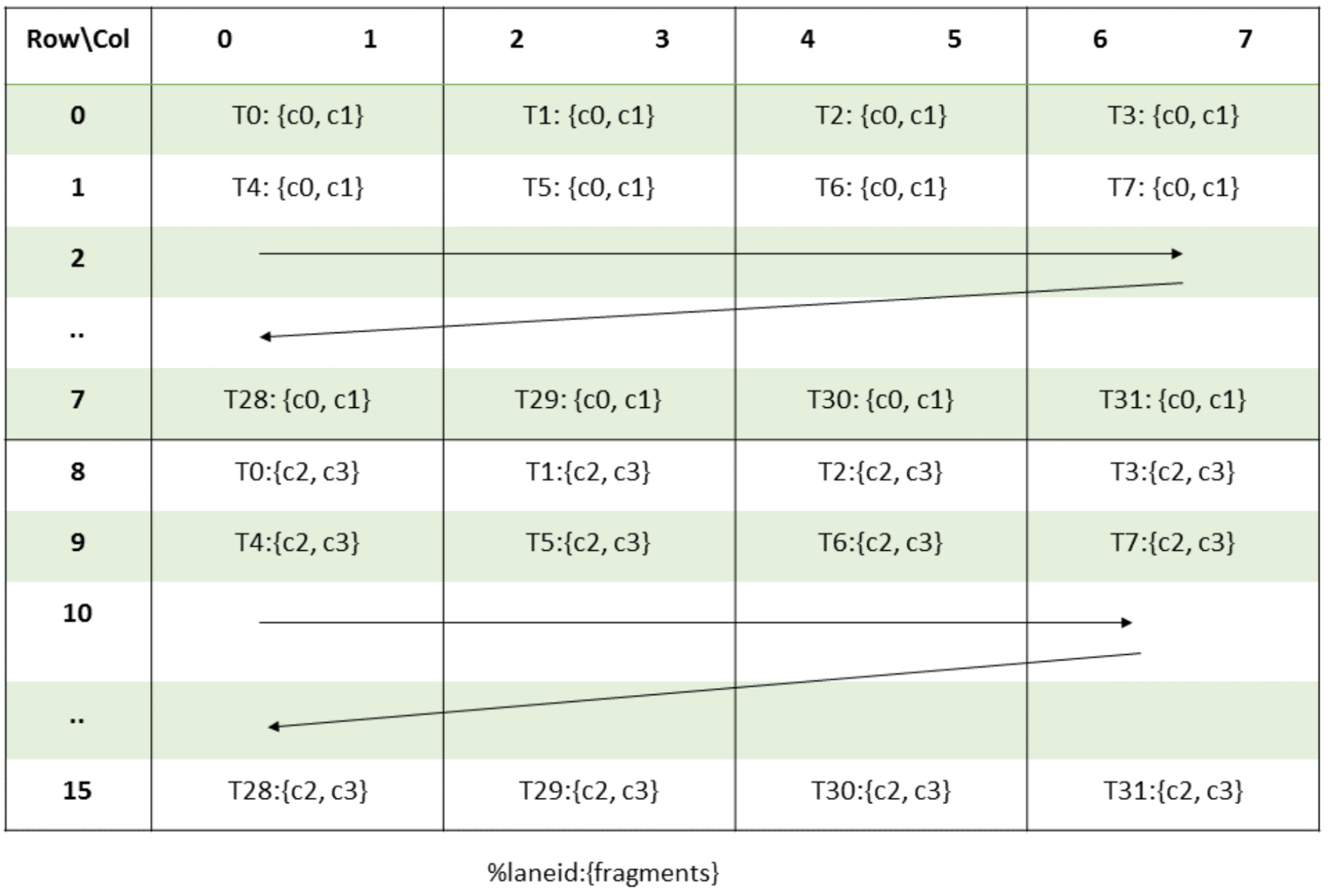
Thread ownership over fp32 elements in register memory for accumulator matrix $D$ would look like:

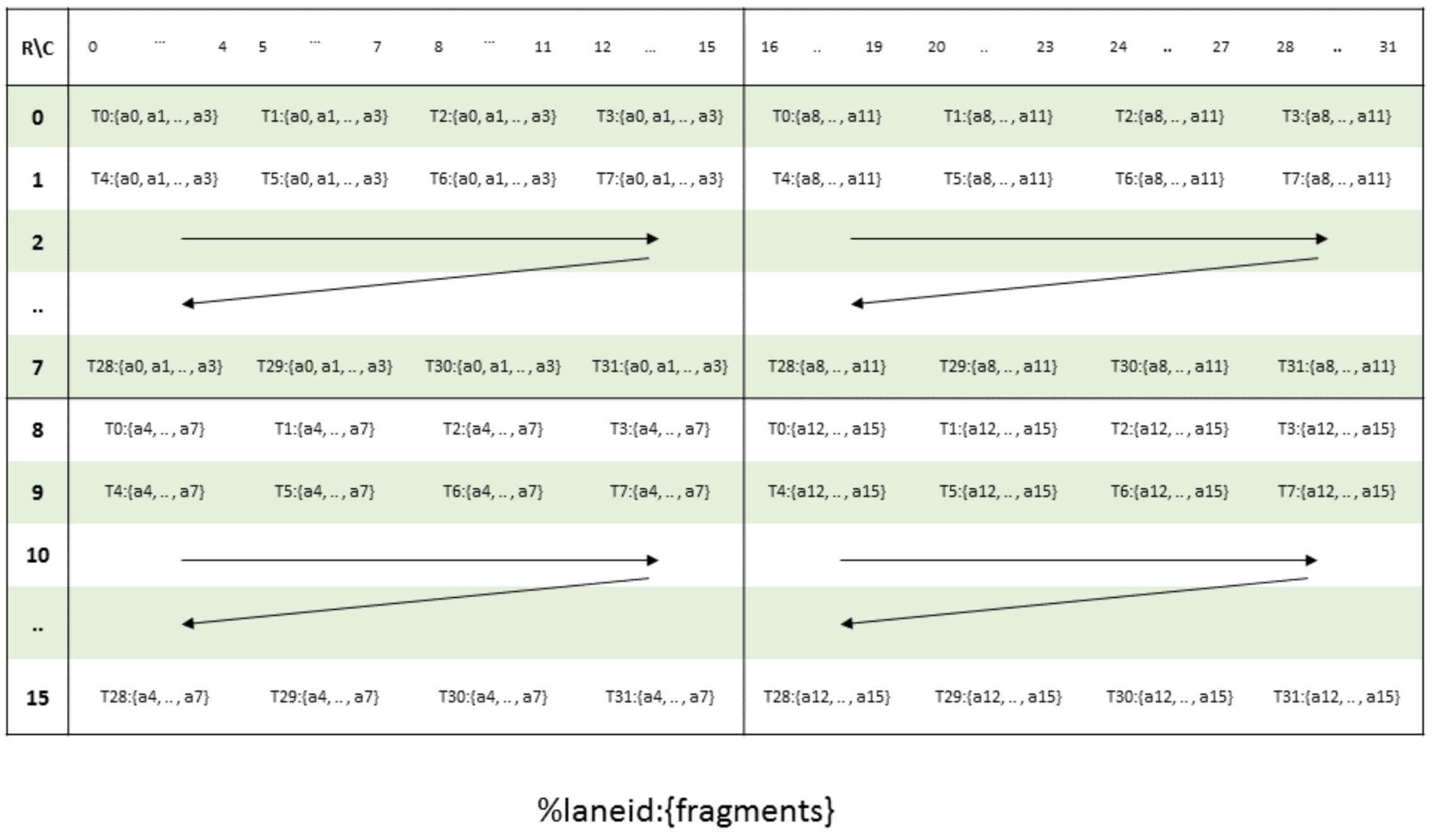
Thread ownership over fp8 data elements register memory for input matrix $A$ would look like:

Now that we've recapped the details, what does this mean for TK? There were two main consequences for our fp8 implementation:

1. The layouts for fp8 are logically distinct. Observe that the bf16/fp16 matrix inputs and the fp32 accumulator use the same logical layout, with two elements per thread, {a0, a1}. However, fp8 packs four elements per thread, {a0, a1, a2, a3}. Therefore, while it is quite easy to swap between fp32/bf16/fp16 layouts, we needed distinct logic to convert between fp32/bf16/fp16 and fp8 precision TK tiles -- we need to shuffle data among threads.

   Each thread can send one value to another thread and obtain one value per shuffle. But:

   • fp8-T1 needs both bf16-T2’s {a0 and a1} and bf16-T3’s {a0 and a1} in order to fill its four elements
   • fp8-T3 needs both bf16-T2’s {a4 and a5} and bf16-T3’s {a4 and a5}

   TLDR: fp8-threads need to obtain values from two threads. bf16-threads need to send values to two different fp8-threads. How can we do this without too many shuffle syncs? Checkout our fp8 conversion function here!

2. These complex matrix layouts mean that when we load data from shared memory to registers, we need to perform tons of expensive address calculations on the GPU’s ALUs. Luckily, NVIDIA provides special instructions to reduce the address calculation cost by $4\times$: the ldmatrix (stmatrix) instruction is designed to help the warp threads collectively load (store) the GEMM matrices from shared memory to registers (registers to shared memory).

   Quick note though: ldmatrix assumes each matrix element holds 16-bits of data (PTX Docs). We want to operate on fp8 (8-bits). To hack around this, in this shared to register load code, we let the instruction load in 16-bits and use this to fill 2 fp8 values per load. One of several hacks the hardware requires users to wrangle with for fp8...

launching warpgroup-level gemms

Modern hardware – NVIDIA H100 GPUs – offer us the exciting ability to launch GEMMs from shared memory as well, executed by a group of four consecutive warps (“warpgroups”). The instruction is called “warpgroup mma” (WGMMA).

Using WGMMAs with shared memory matrices is nice because:

• It offers us the flexibility to save precious, but limited register memory in our kernels, since we don’t need to waste registers on storing the $A$, $B$ GEMM matrices.
• The hardware establishes an asynchronous pipeline between shared and register memory when performing the WGMMA, which helps us hide the register to shared load latencies. WGMMAs use TMA hardware to fetch memory into the tensor cores.

Note that to use a WGMMA instruction, the $A$ matrix can either be in register or shared memory, but the $B$ matrix must be in shared memory.

Shared memory layouts: As a refresher, shared memory is “banked” into $32$ banks of $4$ bytes per bank on modern NVIDIA GPUs: one thread can access the memory in a bank at a time. Therefore, we want to carefully organize the patterns in which we load from shared to register memory so that threads do not try to access the same bank at the same time (called a “bank conflict”).

Again, per bank, there are 4-bytes, or 2 bf16 (2 byte) elements. So naively, if each thread grabs two of these 2 byte elements to pack into a bf16_2 type, going across a single row, then there are no bank conflicts; each thread accesses a different bank – thread 0 grabs the two red boxes, thread 21 grabs the two blue boxes – great!!

If matrix $A$ is in register, the tensor core layout is as we saw in the prior section. However, for the shared memory matrices, we have added constraints on the layouts for tensor core compatibility.

Conceptually, think of each shared memory matrix as broken into “core matrices”, the fundamental compute blocks (atomic unit of computation) for the tensor cores. During our WGMMA, we load shared memory into registers, core-matrix by core-matrix.

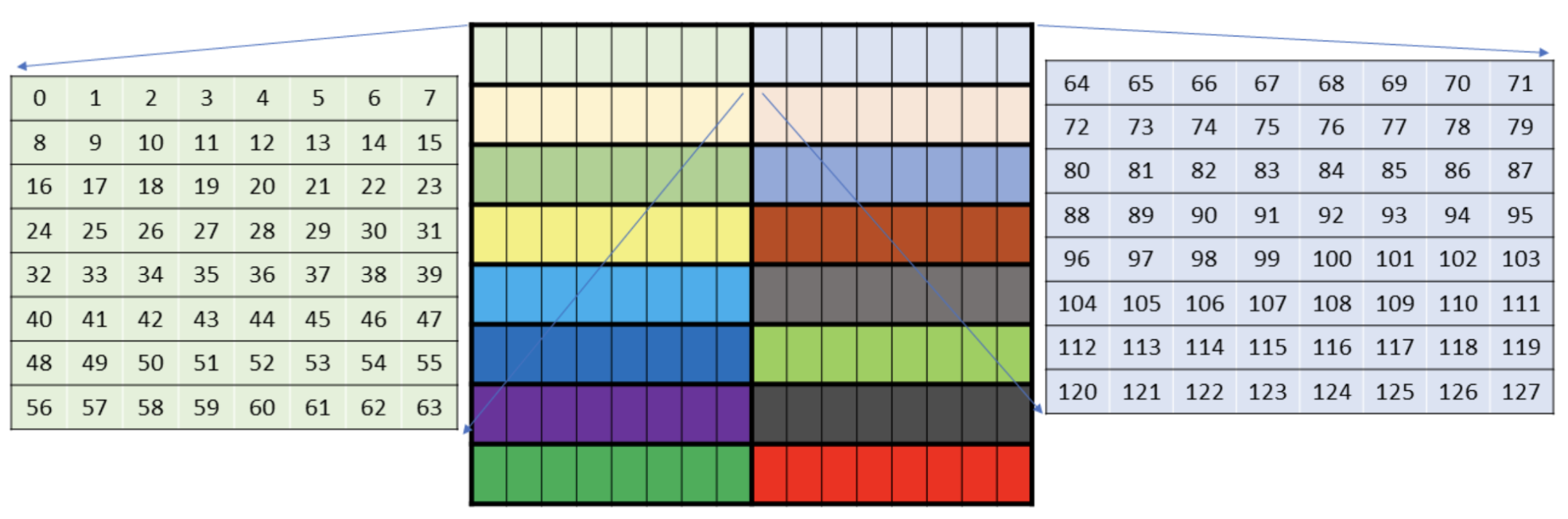
In 16-bit precision, each core matrix has 64 elements of data ($8\times8$ matrix):

Now imagine loading the left core matrix (light green), we can see that 4 threads across will load 2 bf16 elements each (covering the 8 columns). We then have 8 threads per bank (0/1, 8/9, 16/17, 24/25, ..., 56/57) along the row dimension, leading to 8-way bank conflicts. Yikes!

Luckily, the WGMMA instructions allow us to swizzle (or scramble) the addresses during the load, to spread the threads out over the banks as much as possible! For instance below: the light green elements are from banks 0-3, the light blue elements are from banks 4-7. We can see that the threads loading the four green rows will still face conflicts, “4-way bank conflicts”. This swizzle takes regions of 32 bytes (2 green and 2 blue rows) and scrambles them, hence called “32-byte swizzling”. Note that we need our tile to have at least 16 elements across the columns to use this swizzle pattern.

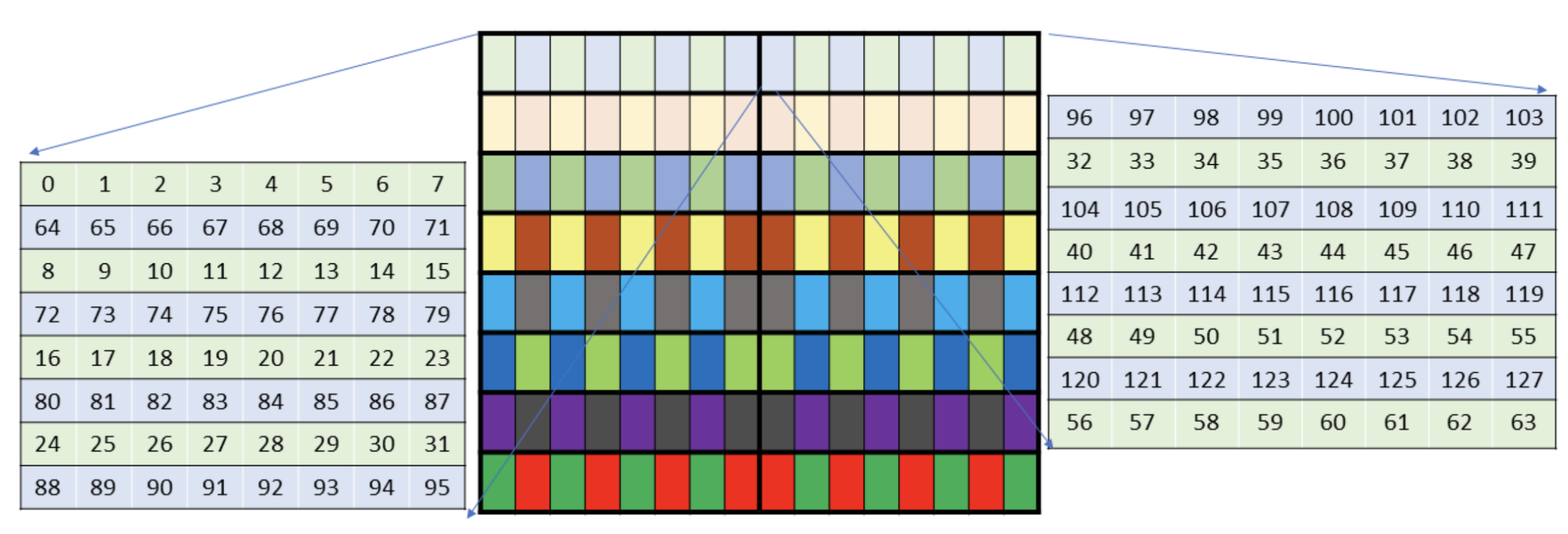
We could also use 64-byte swizzling (on tiles where the width is a multiple of 32 elements), reducing to 2-way conflicts, or 128-byte swizzling (on tiles where the width is a multiple of 64 elements), reducing to 0-way bank conflicts. In the 128-byte depiction below, light green is banks 0-3, light blue is banks 4-7, ..., yellow is banks 24-27, dark red is banks 28-31! Warning: while this diagram suffices for our discussion of bank conflicts, it doesn't give the full picture of how 128-byte swizzling gets handled see more in our earlier post.

Turning back to fp8: in fp8, the core matrices have $8\times16$ elements:

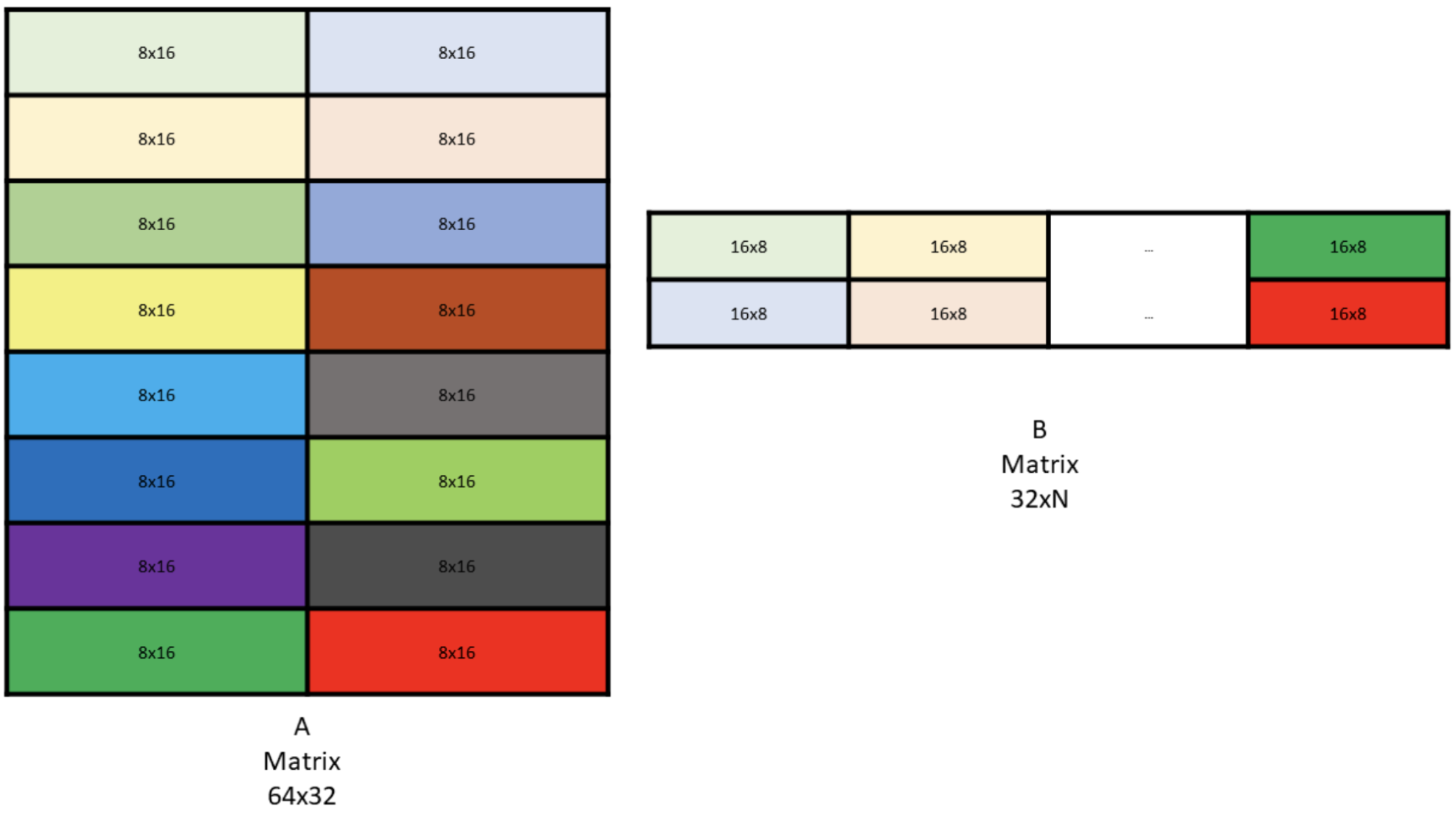
There were a few consequences for our TK tile data structures and downstream fp8 gemm kernel:

To use these three swizzle modes supported by the WGMMAs – 32-byte, 64-byte, and 128-byte – we enforce that the minimum fp8 tile width in TK is 32 elements across (see here at the base level, see here in our core shared tile struct, and see here in our register tile struct). Again, in contrast, the default width for fp16, bf16, and fp32 is 16. We determine which swizzle mode to use for each shared tile here.

Our fp8 GEMM kernel closely resembles our bf16 GEMM kernel on the H100! However, to reduce bank conflicts and use larger swizzle patterns, we set the tile widths for the input $A, B$ matrices to be twice as large. See here in the fp8 kernel and see here in our bf16 kernel! Below, we ablate the width of matrices $A$ and $B$ (32, 64, 128) for our fp8 kernel, modulating the swizzle mode, to provide more intuition on the importance of swizzling and bank conflict avoidance. The hardware utilization increases with the tile width/swizzle!

signing off

That's it for today! We hope TK fp8 helps you build some cool demos; we welcome your contributions and questions! Feel free to reach out on email or our ThunderKittens GPU MODE Discord channel at discord.gg/gpumode!

reference for figures: https://docs.nvidia.com/cuda/parallel-thread-execution/