Just read twice: closing the recall gap for recurrent language models

Full team: Simran, Aman, Aaryan, Ben, Sabri, Xinyi (Jojo), Ashish, Atri, and Chris Ré.

ArXiv | Code | Models

TLDR Today's efficient ML architectures struggle to perform a fundamental skill called associative recall (AR) as well as the de-facto Transformer architecture. AR requires an LM to use info provided in long contexts when generating tokens. The issue is that efficient LMs need to predict what info from long contexts to store in a limited amount of memory. We observe that if prompts are ordered in "the right way" or we use non-causal variants of efficient LMs to process prompts, the prediction problem can become much easier! Our work departs from the modern causal language modeling orthodoxy, where LMs process text left-to-right in a fixed order, to close AR gaps between memory efficient and Transformer LMs.

Introduction

Recent work has made rapid progress in developing fixed-memory recurrent architectures (e.g., Mamba and RWKV) that are competitive with attention in language modeling perplexity. During inference, these models are more memory efficient and asymptotically faster than attention! Amazing, we have quality and efficiency! But what are we missing? As the saying goes, there's no free lunch!

While these LMs are efficient, they make a tradeoff in "associative recall" (AR) ability: they struggle to use information provided in-context when generating responses. Why does this matter? Well while the greater efficiency might be helpful for unlocking long-context applications, such as generating code given an entire codebase, if they can't actually refer to specific functions or variables in context, then that efficiency effectively doesn't matter. We find a popular 2.8Bn parameter Mamba LM trained on 300 Bn tokens of the Pile underperforms a 1.3Bn parameters (2.2× smaller) Transformer LM trained on 50 Bn tokens (6× fewer tokens) by 5 points, averaged across a suite of benchmarks that require AR abilities.

Unfortunately, this fundamental issue for memory-limited LMs: we prove models require $\Omega(N)$ space, in input length N, to solve associative recall tests like the one below. We have a "context" of key-value token pair mappings on the left and "questions" on the right for which the model should output answers $4$, $6$, $1$, $2$, $3$:

Is all lost? This begs the question of whether we can actually rely on the LMs with O(1)-memory recurrent state sizes for language modeling...

Luckily, models often do not need to remember all information provided in-context to excel at a task! The challenge is predicting which subset of information is useful to store. LMs have gotten a lot better at this through innovations on architectural inductive biases like input-dependent decays (e.g., Mamba), LSTM, fast weights, delta rule, etc. Other work like the Based architecture, instead increases the recurrent state size in hardware-efficient and math-guided ways! ^{1 2} Efficient LMs have continued to extend the Pareto frontier of the AR-quality and efficiency tradeoff space, but leave a lot to be desired.

Our insights. We make a simple observation that the order in which a recurrent LM reads input text drastically impacts the difficulty of predicting what to store in the limited memory. Suppose we ask questions $Q$ (e.g., “When did Galileo move to Florence?”), over documents $D$ (e.g., the detailed Wikipedia for Galileo Galilei). The model needs to remember just one fact from $D$ if the prompt is ordered $[Q, D]$, but needs to remember all facts when it is $[D, Q]$. The issue is that essentially all our modern LLMs view text "causally", i.e. they process text in a fixed order – left-to-right. They need to predict the future (predicting that I’ll ask about Galileo’s move to Florence) when deciding what to store (reading Galileo’s page). Note that people don't read like this! We go back and forth and jump around - think back to SAT reading comprehension tests!

Our work goes beyond the causal-LM orthodoxy to close AR gaps to Transformers using efficient recurrent LMs!! We propose two methods in this vein, detailed in the rest of this blogpost:

1. Just read twice prompting (JRT-Prompt): This method repeats the prompt context multiple times before the model needs to generate the answer. It works with any off-the-shelf causal or non-causal model, without modification! With this repeated prompt strategy we can do better than zero-shot Transformers in quality, but with comparable efficiency. You might think the extra context repetition makes things slow, but because we're linear and hardware-efficient we actually end up being faster than the zero-shot Tranformer! We apply JRT-Prompt to $16$ off-the-shelf LMs overall (spanning Based, GLA, Mamba-1, and Mamba-2) resulting in $11.0 \pm 1.3$ points improvement on average across the benchmarks. Based LMs with JRT Prompt can process $32678$ length sequences, $16$ batch size $11.9\times$ faster than Transformers with FlashAttention-2.

2. Just read twice recurrent architecture (JRT-RNN): This architecture uses an encoder-decoder structure to non-causally process prompts then causally decode the answer. JRT-RNN provides $99\%$ of Transformer quality at $360$M params./$30$Bn tokens, averaged across the recall-intensive ICL benchmarks. This represents $46.7\%$ improvement over Based and $78.8\%$ over Mamba. JRT-RNN provides $96\%$ of Transformer quality at $1.3$Bn params. / $50$Bn tokens, representing $16.2\%$ improvement over Based and $34.5\%$ over Mamba on average. Benchmarking our custom CUDA implementation, prefix linear attention can process $32678$ length sequences, $16$ batch size $19.2\times$ faster than FlashAttention-2.

We think there's a lot to do in this space and are interested to hear your feedback on these ideas! At a high level, why are we directly trying to mimic the way we use Transformers with our efficient LMs? We can exploit the asymmetries! Multiple linear passes is asymptotically better than quadratic Transformers!

You can try out our models and hardware-efficient kernels: https://github.com/HazyResearch/prefix-linear-attention.

Understanding the role of data order on efficient models

To demonstrate the sensitivity of recurrent LMs to the data ordering, we started by considering a simplified toy task: the model is given input sequences that contain elements from two sets A and B, and needs to output the tokens in the intersection of $A$ and $B$. E.g., the correct output below would be 6:

Note, that the "set intersection" problem tested by this toy task is a quintessential problem in communication complexity theory that has been studied for decades. The "hardness" of many problems reduces to the hardness of set disjointness (are the two sets disjoint or not)? We also formally show that the associative recall problem reduces to set disjointness problem in our paper!

In evaluating LMs on the toy task, we consider two slices of the test set: when $|A| > |B|$ (“long $A$ to short $B$”) and when $|B| > |A|$ (“short $A$ to long $B$”). We find that causal models achieve better quality when $|B| > |A|$, than when $|A| > |B|$, which is intuitive since the LM needs to store all elements in set A to find the intersection with B. Meanwhile, non-causal LMs outperform when $|A| > |B|$ and match the causal case when $|B| > |A|$! The causal LMs are far more sensitive to the data-ordering (highlighted in the right-hand-side panel).

We theoretically formalize the synthetic observations, pointing to two paths forward to build more reliable $O(1)$-memory recurrent LMs:

1. The causal LM needs $\Omega(\mathrm{min}(|A|, |B|))$ bits of memory to solve set disjointness. Broadly, we should put data in “the right order” in-context (e.g., placing the set with $\mathrm{min}(|A|, |B|)$ first in context). We use this idea in our first proposal, Just read twice prompting.

2. We prove non-causal LMs can solve set disjointness in $\Omega(\mathrm{min}(|A|, |B|))$ bits of memory, regardless of the data order in context. We use this idea in our second proposal, the Just read twice recurrent architecture.

Just read twice prompting

Just read twice is very simple: we just repeat the prompt (e.g., document and question) multiple times in context before the model generates an answer. Intuitively, in the second (or subsequent) pass over the context, the LM can condition on the full context to decide what to store in the state -- we get around the issue of needing the data to be in "the right order"!

We take $16$ pretrained recurrent LMs from Hugging Face and evaluate them using standard zero-shot prompting versus JRT-prompts on six recall-intensive tasks (document question answering, information extraction). Each cell below shows the Standard / JRT scores respectively.

Architecture	Params	Tokens	FDA	SWDE	NQ	SQUADv2	TriviaQA	Drop
Transformer	1.3B	10B	74.4 / 86.1	41.4 / 52.5	28.2 / 31.9	39.0 / 53.1	49.5 / 49.3	22.3 / 33.6
Mamba	1.3B	10B	23.3 / 40.3	15.5 / 31.8	19.4 / 25.8	26.6 / 48.5	46.4 / 51.1	21.3 / 32.1
Based	1.3B	10B	48.6 / 58.9	27.6 / 44.7	19.7 / 28.4	31.0 / 46.7	44.1 / 51.9	19.5 / 34.6
Transformer	1.3B	50B	83.7 / 89.2	50.8 / 65.0	32.8 / 37.5	41.1 / 58.1	56.6 / 58.8	21.5 / 37.9
Mamba	1.3B	50B	41.9 / 55.7	32.6 / 45.4	26.9 / 33.9	31.5 / 53.5	54.9 / 56.7	20.4 / 33.8
Based	1.3B	50B	60.2 / 68.3	37.1 / 54.0	29.4 / 35.2	38.9 / 56.3	54.5 / 57.6	21.7 / 39.1
Mamba	130M	300B	25.7 / 32.8	17.5 / 31.5	16.8 / 21.7	27.1 / 51.9	43.5 / 50.1	17.4 / 30.7
Mamba	370M	300B	41.9 / 58.3	27.6 / 42.2	23.8 / 31.1	34.9 / 51.0	53.6 / 51.7	19.3 / 33.2
Mamba	1.4B	300B	45.8 / 60.9	37.6 / 46.0	31.0 / 36.6	39.9 / 59.6	60.5 / 61.3	20.9 / 36.4
Mamba	2.8B	300B	54.3 / 66.6	38.9 / 48.9	33.5 / 40.1	43.9 / 59.4	66.2 / 63.9	19.8 / 36.9
GLA	1.3B	100B	48.3 / 68.6	37.7 / 53.6	26.6 /  31.1	34.7 / 54.8	55.5 / 54.6	17.4 / 30.7
GLA	2.7B	100B	47.1 / 65.8	43.6 / 54.5	27.1 / 32.9	37.2 / 55.7	57.9 / 57.0	22.2 / 34.0
Mamba2	130M	300B	32.2 / 50.9	29.5 / 43.3	20.6 / 28.9	30.4 / 47.0	43.7 / 47.2	18.0 / 34.0
Mamba2	370M	300B	60.8 / 76.7	38.3 / 52.1	26.6 / 33.6	35.3 / 51.8	54.6 / 54.7	22.4 / 36.3
Mamba2	1.3B	300B	66.8 / 74.7	50.0 / 59.6	33.6 / 40.5	42.9 / 59.6	63.8 / 62.4	23.2 / 36.6
Mamba2	2.7B	300B	68.7 / 81.6	55.2 / 60.8	34.4 / 41.7	45.4 / 59.4	66.4 / 66.5	23.0 / 42.5

This results in $11.0 \pm 1.3$ points of accuracy improvement on average for non-Transformer LMs across the benchmarks. Checkout our paper for more analysis. We show JRT outperforms few-shot prompting, and the full repetition also appears to be more helpful than only repeating the question.³ These results highlight that LMs are brittle across varied data orderings in context.

JRT prompt with two repetitions does double the context length, but using recurrent LMs, this is still asymptotically more efficient than the quadratic scaling of Transformers. Interestingly, a lot of our work on efficient LMs tries to directly mimic the experience of using Transformers, but we could exploit the asymmetry: multiple linear passes can still be better than one quadratic pass in many regimes. We're excited for future methods along this line of thinking.

Benchmarking our hardware-efficient implementation of Based, written in the ThunderKittens framework, JRT-Prompt applied to Based models can provide 11.9X higher throughput than FlashAttention-2 at sequence length $32768$ and batch size $16$ on an NVidia H100 GPU. It is also worth re-emphasizing that JRT-Prompt can be used with any off-the-shelf LM.

Just read twice recurrent architecture

We have shown that the recall quality of causal recurrent LMs varies depending on the order in which the information appears in context, making them brittle for in-context learning. In our set disjointness analysis, we found that non-causal recurrent LMs could help! If a LM can non-causally view the entire prompt context when deciding what information to store or discard, the LM may be able to make better selection decisions.

A long line of work has demonstrated the strength of non-causal "bidirectional" neural networks in language modeling. However, it is challenging to use them for fast text generation because the context must be re-processed for each generated token to achieve good quality. Encoder-decoder architectures with a bidirectional encoder and causal decoder offer a way to achieve fast causal generation while reaping the benefits of bidirectional LMs. Nonetheless, decoder-only causal autoregressive LMs remain the norm and encoder-decoder architectures have received little attention in the context of sub-quadratic efficient LMs.

We propose a simple encoder-decoder architecture, JRT-RNN, that goes beyond the de-facto causal modeling! We'll start by defining some baseline efficient LMs for the causal setting and then describe our approach.

Preliminaries in the causal case

Sequence mixers are the part of an LM that determines how words in input $x \in \mathbb{R}^{N \times d}$ for sequence length $N$ and model dimension $d$, interact with each other when computing output representations $y \in \mathbb{R}^{N \times d}$ for the subsequent layer of a deep neural network.

First we'll start with the de-facto attention (Bahdanau et al., 2014) sequence mixer and then describe a popular category of efficient LMs, which uses linear attention (Katharopoulos et al., 2020). Linear attention is closely related to another popular category of efficient LMs based on state space models (Gu et al., 2021).

Attention models mix tokens as follows:

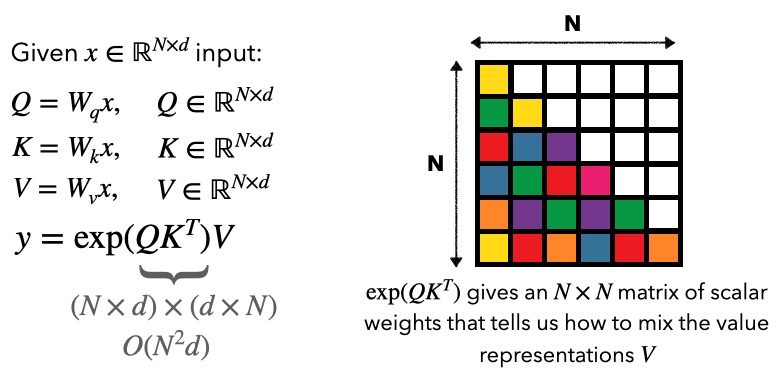
Attention takes $O(N^2d)$ compute and linear $O(Nd)$ memory during training. In inference, remember we generate one token at a time $t$ -- each new query $Q_t$ needs to interact with all the prior $K_{0:t}$ and $V_{0:t}$ so if we cache those keys and values, compute and memory to generate a token scales with $t$.

Linear attention models replace the $\exp$ with a “feature map” $\phi: \mathbb{R}^{N \times d'} \rightarrow \mathbb{R}^{N \times D}$, with “feature dimension” $D$. As before, $d$ is the model dimension, but we’ll decouple $d’$ so $Q$ and $K$ can be projected to a different dimension than $V$ as needed.

Shown in the figure, this is now $O(NDd)$ linear in $N$ during training. During inference, by summing prior $h_t = \sum_{i=0}^{t} \phi(K_t^T) V_t$ such that $h_t \in \mathbb{R}^{1 \times Dd}$, then multiplying this with $Q_t$, observe our compute and memory to generate a token is constant $O(1)$ as $t$ grows!

Our approach

Prefix linear attention. We first uses what we refer to as prefix linear attention (PLA), inspired by the class of prefix LM architectures. We split the sequence into two regions: a non-causal encoder region of length $M$, $M < N$ and a causal decoder region of length $N-M$. Adding projections to compute $A_e$, $B_e$ on the encoder side, we compute outputs as:

Like standard linear attention, PLA is agnostic to the choice of feature map $\phi(\cdot)$. Observe that PLA retains the compute complexity and recurrent state size of causal linear attention during decoding, but processes the "prompt region" (first $M$ tokens) twice during prefill.

We introduce a hardware efficient CUDA implementation using the ThunderKittens CUDA library for PLA, which takes just $1.24\times$ the time of the baseline decoder linear attention LM. In benchmarking, this implementation provides $19.2\times$ higher $19.2\times$ higher throughput than FlashAttention-2 for prefill of length $32K$, batch size $16$!

Pretraining Loss. Decoder-LMs are trained using a next token prediction loss: i.e, at each position $i$ in the sequence, the LM uses tokens $0-i$ to predict token $i+1$. In PLA, we can’t compute a NTP loss for tokens 1 through M since the model views them non-causally. Instead, we use a masked language modeling loss for tokens in the encoder region (i.e., replacing / "masking" some words in the sequence and measuring how well the model predicts the original word that got masked) plus next token prediction loss in the causal decoder region (last $N-M$ tokens). Note that if we mask roughly $15\%$ of tokens, let $M = \frac{N}{2}$, and normalizing for the total number of input sequences, the non-causal JRT LM would compute losses on roughly $65\%$ the number of tokens of the causal LMs. However, how best to normalize training across causal vs. non-causal models is an open question that we hope future work will continue to engage with.

Results

On the set of recall-intensive benchmarks, JRT-RNN provides consistent improvements over strong decoder recurrent LM baselines, achieving 96% the quality of the very strong Transformer ++ (Llama architecture) baseline! We compare to two very strong $O(1)$-memory recurrent LM baselines: JRT gives a $16.2\%$ improvement over the Based baseline and $34.5\%$ improvement over the Mamba baseline at $1.3$Bn parameters and $50$Bn tokens. Checkout our paper for lots more results and analysis!

Architecture	Params/Tok	FDA $N=512$	FDA $N=512$	SWDE $N=512$	SWDE $N=512$	NQ $N=512$	NQ $N=512$	SQUADv2	TriviaQA	Drop	Avg.
Transformer	1.3B/50B	85.6	83.5	55.7	56.0	33.4	29.9	40.1	56.6	21.4	51.4
Mamba	1.3B/50B	55.4	40.1	44.0	33.7	27.6	23.2	32.2	54.5	20.7	36.8
Based	1.3B/50B	69.3	58.8	47.6	40.4	29.1	24.4	38.5	54.3	20.8	42.6
JRT-RNN	1.3B/50B	86.7	67.7	49.4	45.7	38.3	25.4	50.4	53.0	29.3	49.5

Overall, nearly all the focus on efficient attention alternatives LMs has been on decoder-only LMs. We're very excited about the potential of (1) non-causal modeling and (2) making multiple linear passes over the input prompt as two ways to help make efficient LMs competitive with Transformers on the important recall skill, and think there are so many more ideas to consider along these directions. ⁵

If you’re interested in chatting more about any of these topics, please feel free to reach out at: simarora@stanford.edu. We'd like to thank Hazy Research, Cartesia, and Together for supporting our work!

Finally, big thank you to labmates including Michael Zhang, Dan Fu, Neel Guha, and Jon Saad-Falcon on helpful feedback on this blogpost and the overall work!