Feb 15, 2023 · 6 min read
Simple Long Convolutions for Sequence Modeling
Dan Fu, Elliot Epstein, Eric Nguyen, Armin Thomas, Michael Zhang, Tri Dao, Atri Rudra, and Chris Ré.
Over the past couple years, we’ve been studying how to get good performance on sequence modeling, and developing both new systems techniques and new deep learning architectures to get there. Today, we’re going to take a look at a simple baseline that can do surprisingly well: just use a long convolution the size of the input sequence! It turns out that we just need a simple regularization, and then convolutions can match more complicated sequence models like S4 on benchmarks like the Long Range Arena and text modeling.
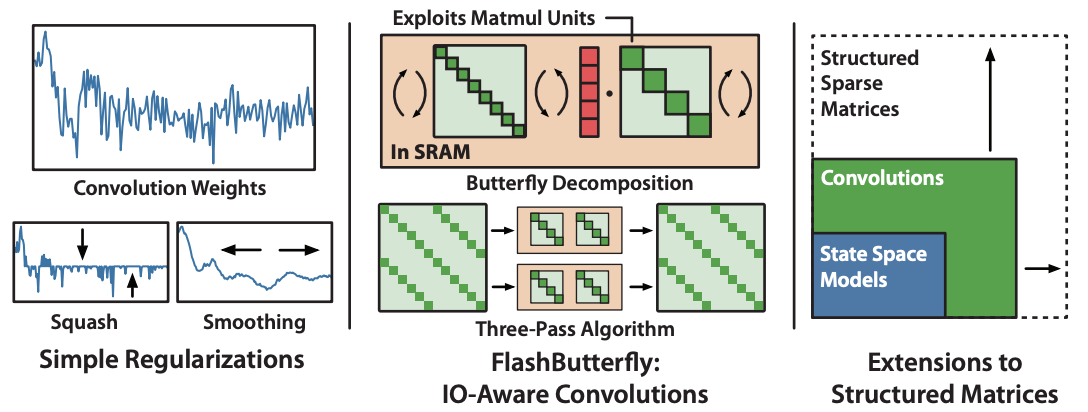
Simple long convolutions for sequence modeling. We focus on the kernel regularization in this blog post, but you can read more about FlashButterfly and connections to structured sparsity in our paper.
A fundamental research question is – what is the simplest architecture that can get good quality on tasks that we care about? Over the past couple of years, our lab has been spending a lot of time studying sequence modeling. And we’ve seen that deep state space models (SSMs) like S4 are a good architecture for sequence modeling – with very strong performance on the long range arena benchmark, text modeling, and more.
But SSMs are a bit complex - to train in a modern deep learning stack, they rely on sophisticated mathematical structures to generate a convolution kernel as long as the input sequence. This process can be unstable, and requires careful initialization for good quality.
So this complexity naturally raised a question for us - is there a simpler approach that can still get good quality on sequence modeling? There’s a natural candidate to look at: since SSMs have to generate a convolution kernel, why not parameterize the convolution kernel directly?
In our new paper, we show that directly parameterizing the convolution kernel works surprisingly well – with a twist! We need to add a simple regularization, and then long convolutions can match SSMs in quality. We also show in the paper that there is a deep connection between these methods and structured sparse GEMMs using the theory of Monarch matrices – check it out for more details!
Regularizing Long Convolutions
The first question we asked was – what happens if you just replace the SSMs with long convolutions? The code is pretty simple, and we can use the FFT convolution to compute a long convolution in time (instead of , as you might find in PyTorch Conv1D):
def init(L):
self.kernel = nn.Parameter(L)
def forward(x):
# Compute convolution with FFT
return torch.fft.irfft(torch.fft.rfft(x) * torch.fft.rfft(self.kernel))
But if you try this on a benchmark like LRA, you quickly find that performance lags behind S4:
| Model | LRA Average Acc |
|---|---|
| S4 | 86.1 |
| Long Convolutions | 69.5 |
Why is that the case? If you visualize the kernels that you learn, something begins to pop out as a potential answer -- the long convolution kernels are super non-smooth and noisy!
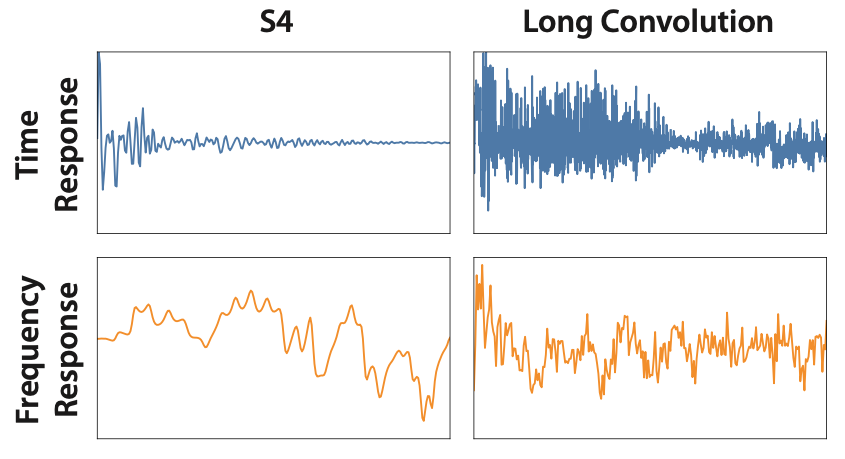
Convolution kernels compared to S4. Time response on top, frequency response on bottom.
We found that applying a simple regularization – a Squash operator – to the kernel weights could solve this. It’s super simple in code, and just introduces one hyperparameter :
def init(L, lambda):
self.kernel = nn.Parameter(L)
self.lambda = lambda
def forward(x):
# Squash the kernel
k = torch.sign(k) * torch.relu(torch.abs(self.kernel) - self.lambda)
# Compute convolution with FFT
return torch.fft.irfft(torch.fft.rfft(x) * torch.fft.rfft(k))
If you apply this operator during training, you get kernels that are much sparser in time domain, and smoother in frequency domain:
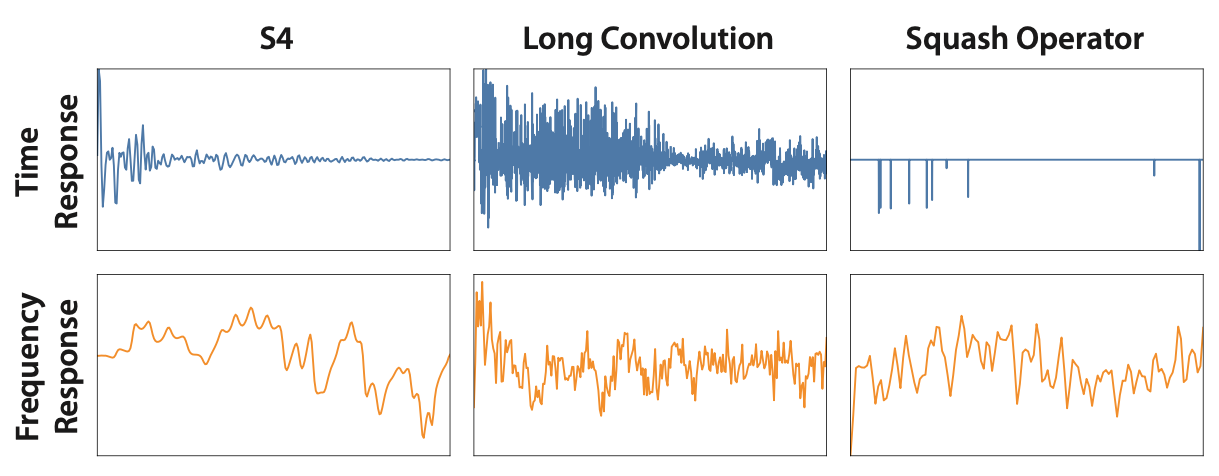
Convolution kernels, with the squash operator. Much sparser in the time domain, and smoother in frequency space!
And if you benchmark this on LRA, you see that this little change is all you need to match the performance of S4:
| Model | LRA Average Acc |
|---|---|
| S4 | 86.1 |
| Long Convolutions | 69.5 |
| Long Convolutions + Squash | 86.1 |
That was pretty exciting for us, so our next question was how well these results would generalize to other settings. We evaluated image classification, text modeling, and brain fMRI analysis in our paper, and found that long convolutions did pretty well across all those settings. Since we’ve been talking a bit about H3 in this blog post, we’ll just leave you with an exciting result on text modeling.
We took the H3 layer – which stacks two SSMs and runs multiplicative interactions between them – and replaced the SSMs with convolutions. When we trained this new H3-Conv model on the PILE, we found that it matched the performance of H3, and outperformed Transformers – exciting stuff!
| Train Tokens | 5B | 10B | 15B |
|---|---|---|---|
| Transformer | 12.7 | 11.3 | 10.7 |
| H3 | 11.8 | 10.7 | 10.2 |
| H3-Conv | 11.9 | 10.7 | 10.3 |
What's Next
This is just a preview of what you’ll find in our paper – be sure to check it out for more:
- Evaluations of long convolutions in more settings – fun applications like image classification and brain fMRI analysis!
- New systems optimizations to improve the runtime performance of long convolutions – we’re able to show 1.8X faster runtime than the most optimized SSM implementations at sequence length 128K, since we don’t have to generate the convolution kernel from SSM parameters.
- An interesting connection to the theory of Monarch matrices! Turns out we can replace parts of the convolutions with structured sparse GEMMs. This gives us some more expressivity – we can stick extra parameters into the GEMM without costing more compute, and we get a bit better quality almost for free.
There are also some nice properties of SSMs that we don’t get when we go to a simpler formulation, that we’d love to explore more in the future.
- For example, SSMs have very fast generative inference, since you can cache the hidden state.
- And SSMs can have parameter count independent of sequence length (in our simple formulation, parameters grow linearly with sequence length).
- SSMs also naturally extend to multiple resolutions through re-sampling the state matrix.
We’re very interested in seeing how to get simple long convolutions to have similar properties!
We’re very excited about these directions, and we’re very excited about developing them in the open. If you’re excited about these ideas too, please reach out!
Dan Fu: danfu@cs.stanford.edu; Elliot Epstein: epsteine@stanford.edu