Jan 17, 2022 · 7 min read

Pixelated Butterfly: Simple and Efficient Sparse Training for Neural Network Models

Our paper Pixelated Butterfly: Simple and Efficient Sparse Training for Neural Network Models is available on arXiv, and our code is available on GitHub.

Why Sparsity?

Recent results suggest that overparameterized neural networks generalize well (Belkin et al. 2019). We've witnessed the rise and success of large models (e.g., AlphaFold, GPT-3, DALL-E, DLRM), but they are expensive to train and becoming economically, technically, and environmentally unsustainable (Thompson et al. 2020). For example, a single training run of GPT-3 takes a month on 1,024 A100 GPUs and costs $12M. An ideal model should use less computation and memory while retaining the generalization benefits of large models.

The simplest and most popular direction is to sparsify these models -- sparsify matrix multiplications, the fundamental building blocks underlying neural networks. Sparsity is not new! It has a long history in machine learning (Lecun et al. 1990) and has driven fundamental progress in other fields such as statistics (Tibshirani et al. 1996), neuroscience (Foldiak et al. 2003), and signal processing (Candes et al. 2005). What is new is that in the modern overparameterized regime, sparsity is no longer used to regularize models -- sparse models should behave as close as possible to a dense model, only smaller and faster.

What are the Challenges?

Sparse training is an active research area, but why has sparsity not been adopted widely? Below we summarize a few challenges that motivate our work:

Choice of Sparse Parameterization: Many existing methods, e.g., pruning (Lee et al. 2018, Evci et al. 2020), lottery tickets (Frankle et al. 2018), hashing (Chen et al. 2019, Kitaev et al. 2020) maintain dynamic sparsity masks. However, the overhead of evolving the sparsity mask often slows down (instead of speeds up!) training.
Hardware Suitability: Most existing methods adopt unstructured sparsity, which may be efficient in theory, but not on hardware such as GPUs (highly optimized for dense computation). An unstructured sparse model with 1% nonzero weights can be as slow as a dense model (Hooker et al. 2020).

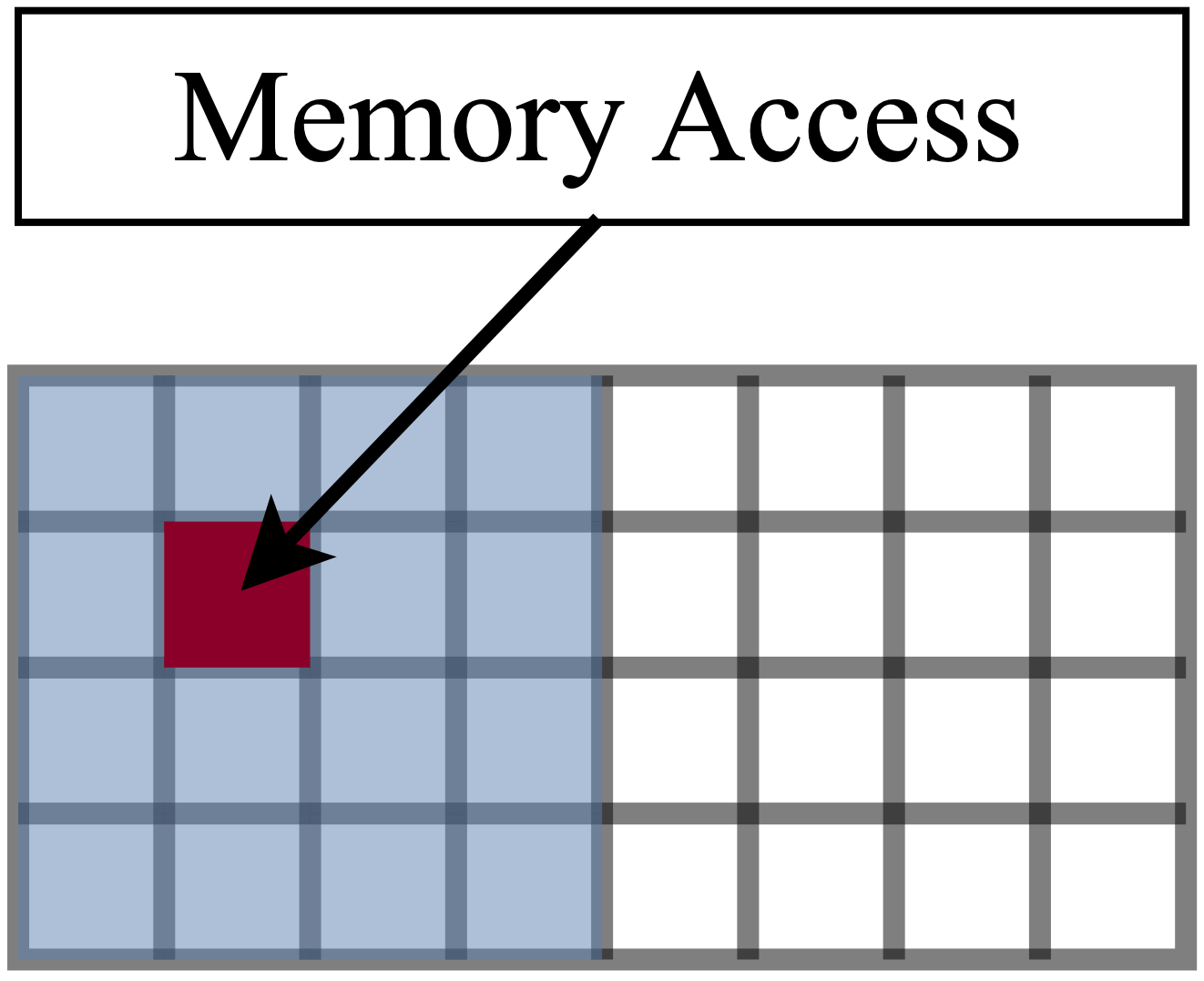
Memory access for a hardware with block size 16: one (red) location access means full 16 $\times$ (blue) access.

Layer Agnostic Sparsity: Most existing work targets a single type of operation such as attention (Child et al. 2019, Zaheer et al. 2020), whereas neural networks often compose different modules (attention, MLP). In many applications the MLP layers are the main training bottleneck (Wu et al. 2020).

Therefore, we are looking for simple static sparsity patterns that are hardware-suitable and widely applicable to most NN layers.

Our Approach: Pixelated Butterfly

Intuition: In our early exploration, we observe that one sparsity pattern: butterfly + low-rank, consistently outperforms the others. This "magic" sparsity pattern closely connects to two lines of work in matrix structures (see Figure 1):

Sparse + low-rank matrices (Candes et al. 2011, Udell et al. 2019, Chen et al. 2021): can capture global and local information,
Butterfly matrices (Parker et al. 1995, Dao et al. 2019): their products can tightly represent any sparse matrices with near-optimal space and time complexity. With butterfly, we can avoid the combinatorial problem of searching over all the possible sparsity pattern!

Butterfly + low-rank is static and applicable to most NN layers.

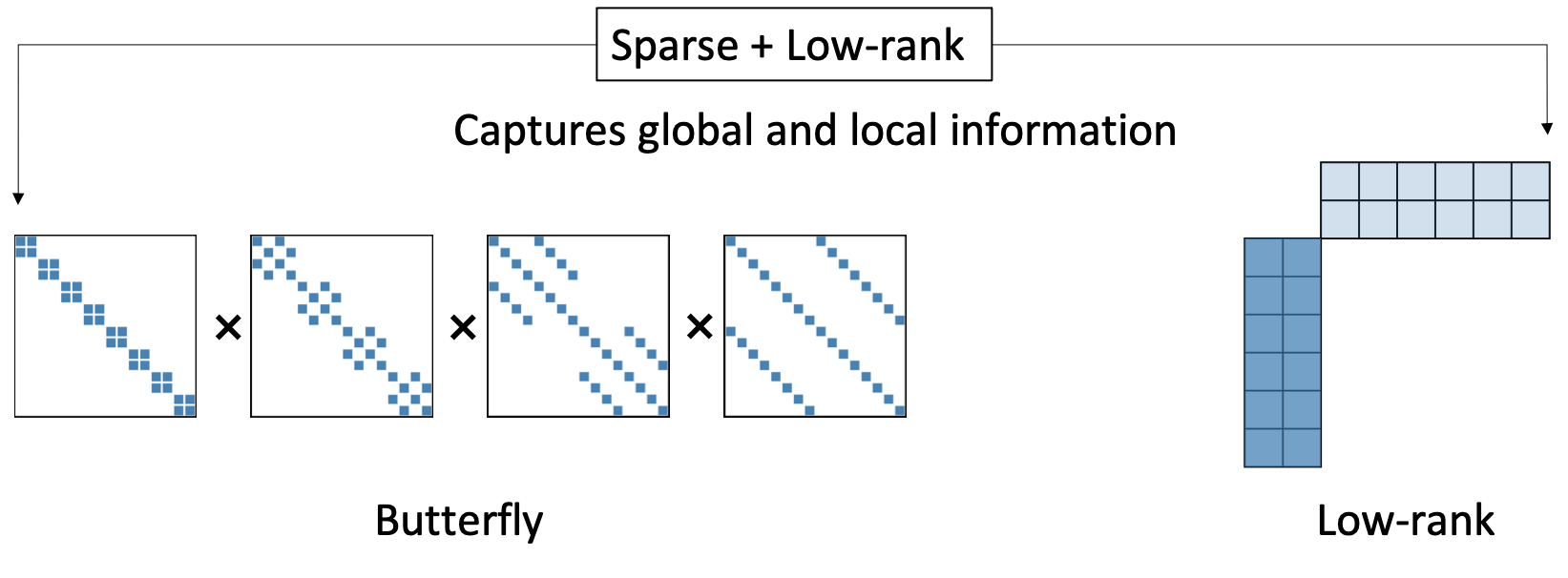
Figure 1: Observation - Butterfly + Low-rank is a simple an effective fixed sparsity pattern.

However, butterfly matrices are inefficient on modern hardware because (1) their sparsity patterns are not block-aligned, and (2) they are products of many factors -- hard to parallelize.

We address the issues with two simple changes (see Figure 2).

Block butterfly matrices operate at the block level, yielding a block-aligned sparsity pattern.
Flat butterfly matrices are first-order approximation of butterfly with residual connection, that turns the original product of factors into a sum.

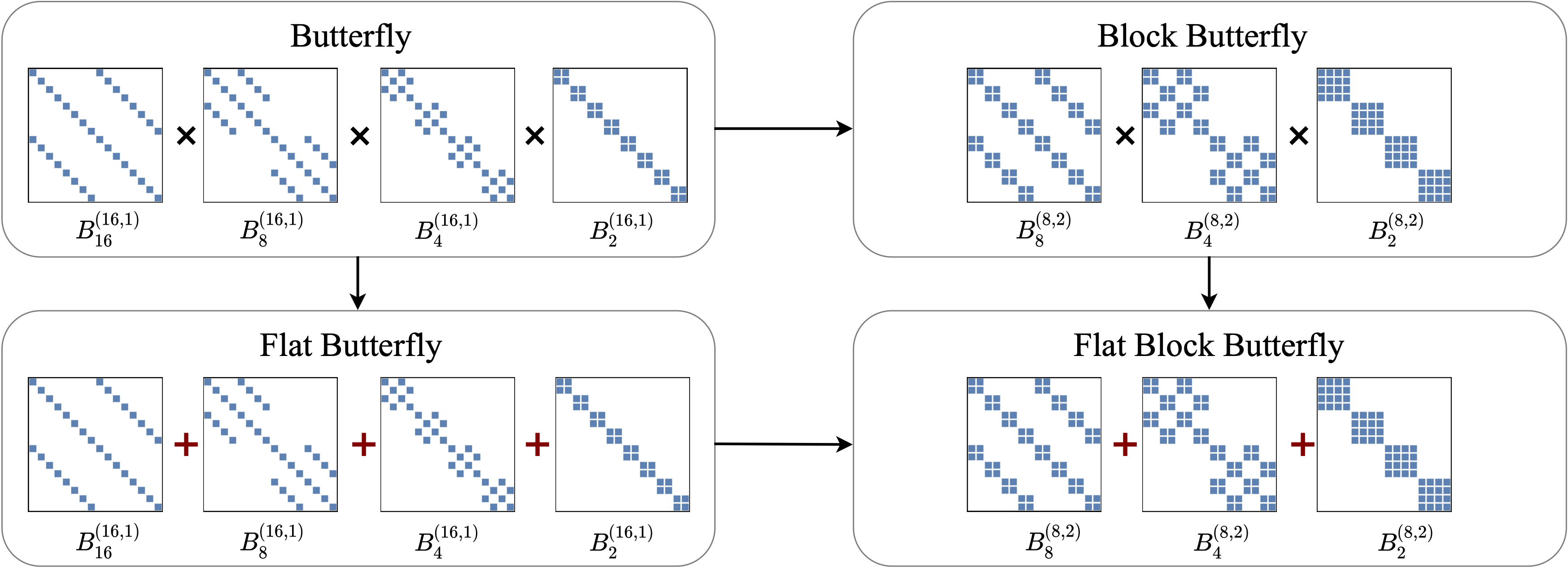
Figure 2: Visualization of Flat, Block, and Flat Block butterfly.

One last problem is that Flat butterfly matrices are necessarily high-rank and cannot represent low-rank matrices. The good news is we have a low-rank term that can increase expressiveness of Flat butterfly!

Putting everything together: Our proposal, Pixelated Butterfly, combines Flat Block butterfly and low-rank matrices to yield a simple and efficient sparse training method (see Figure 3). It applies to most major network layers that rely on matrix multiplication.

Figure 3: Pixelfly targets GEMM-based networks, which it views as a series of matmul. For each matmul from Schema, it (1) allocates compute budget based on dimension and layer type, (2) decides a mapping to our proposed flat block butterfly sparsity patterns, (3) outputs a hardware-aware sparse mask.

What do we get?

In short: up to 2.5 $\times$ faster training MLP-Mixer, ViT, and GPT-2 medium from scratch with no drop in accuracy.

Details: Pixelfly can improve training speed of different model architectures while retaining model quality on a wide range of domains and tasks (both upstream and downstream).

Image classification: We train both MLP-Mixer and ViT models from scratch up to 2.3 $\times$ faster on wall-clock time with no drop in accuracy compared to the dense model and up to 4 $\times$ compared to RigL and BigBird sparse baselines.

Model	ImageNet (top-1 acc. ↑)	Speedup	Params	FLOPs
Mixer-B/16	75.6	-	59.9M	12.6G
Pixelfly-Mixer-B/16	76.3	2.3 $\times$	17.4M	4.3G

ViT-B/16	78.5	-	86.6M	17.6G
Pixelfly-ViT-B/16	78.6	2.0 $\times$	28.2M	6.1G

Language modeling & text classification: We speed up GPT-2 medium dense model training by 2.5 $\times$ , achieving a perplexity of 22.5 on wikitext-103 and 5.2 $\times$ speed-up on Long Range Arena (LRA) benchmark.

Model	WikiText-103 (ppl ↓)	Speedup	Params	FLOPs
GPT-2-medium	20.9	-	345M	168G
Pixelfly-GPT-2-medium	21.0	2.5 $\times$	203M	27G

Downstream tasks: We train Pixelfly-GPT2-small on a larger scale dataset, OpenWebText, and evaluate the downstream quality on zero-shot generation and classification tasks (EleutherAI Repo, Zhao et al. 2021), achieving comparable and even better performance to the dense model.

Model	Classification (avg acc ↑)	WikiText (ppl ↓)	Lambada (acc ↑)	Params
GPT-2-small	31.8	38.3	30.5	117M
Pixelfly-GPT-2-small	32.1	38.3	32.5	82M
GPT-2-medium	33.2	31.87	35.4	345M
Pixelfly-GPT-2-medium	33.4	30.5	38.9	203M

Sparsity: The Way Forward

Our method is a first step towards the goal of making sparse models train faster than dense models and make them more accessible to the general machine learning community. We are excited about several future directions.

Pixelfly 2.0: Pixelfly is a simple first order approximation of the rich class of butterfly matrices, and there could be better approximations or even an exact hardware-efficient re-parameterization.
Going beyond dense models: Many algorithms for exploiting model sparsity have long been used in scientific computing, e.g., locality sensitive hashing, butterfly factorization. Sparse models might unlock tremendous performance improvements in applications such as PDE solving and MRI reconstruction.
Algorithm-Hardware Co-design: Inspired by the remarkable success of model pruning for inference, it is possible that dynamic block sparse mask could be made efficient yet still accurate on the next generation of ML accelerators.
Data Sparsity: In the near future (or now), there will be a swing from model-centric to data-centric AI, where the focus is to study how data can shape and systematically change what a model learns (see this blog). It is possible that a subset of training data is necessary for a model to maintain accuracy or quality, which can speed up training from a different angle!

Stay tuned!